题目
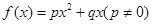 ,其导函数为
,其导函数为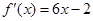 ,数列
,数列 的前
的前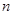 项和为
项和为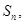 点
点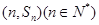 均在函数
均在函数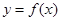 的图像上;.
的图像上;.(Ⅰ)求数列
 的通项公式;
的通项公式;(Ⅱ)若
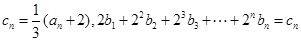 ,求数列
,求数列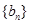 的通项公式;
的通项公式;
答案
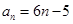 ;(Ⅱ)
;(Ⅱ)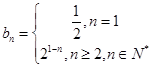 。
。
解析
(1)根据已知条件,二次函数
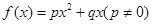 ,则
,则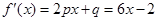
故
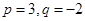 所以
所以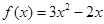 ,点
,点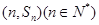 均在函数
均在函数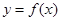 的图像上,
的图像上,则
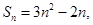 利用通项公式与前n项和的关系式得到通项公式的求解。
利用通项公式与前n项和的关系式得到通项公式的求解。(2)由(Ⅰ)得,
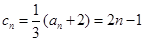 ,
,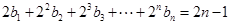 ,利用整体的和式,相减得到通项公式。
,利用整体的和式,相减得到通项公式。解:(Ⅰ)已知二次函数
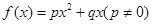 ,则
,则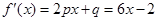
故
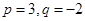 ……………………………2分
……………………………2分所以
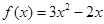 ,点
,点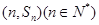 均在函数
均在函数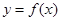 的图像上,
的图像上,则
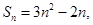 当
当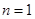 时,
时,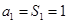 ;当
;当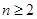 时,
时,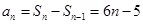 ……5分
……5分故数列
 的通项公式:
的通项公式: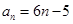 ………………………………6分
………………………………6分(Ⅱ)由(Ⅰ)得,
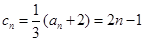 ,
,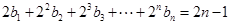 ,
,当
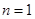 时,
时,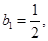 …………………………………7分
…………………………………7分当
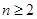 时,
时,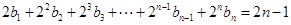
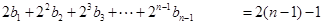
两式相减得:
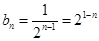 ,……………………………………11分
,……………………………………11分故数列
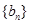 的通项公式:
的通项公式: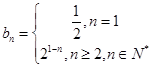 ……………………………12分
……………………………12分
