题目

（本小题满分12分）
已知二次函数.
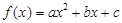（1）若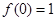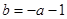，，解关于x不等式;
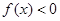（2）若f(x)的最小值为0，且A.<b，设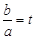，请把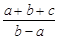表示成关于t的函数g(t)，并求g(t)的最小值.

答案

(1)当A.>1时,解为： 1/A.<x<1 当A.=1时，解为空集。
当0<A.<1时,解为： 1<x<1/A.当A.=1时, 解为 x>1
当A.<0时,解为： x>1或x<1/A.。
（2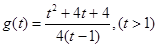） 最小值为3

解析

本试题主要是考查了一元二次不等式的求解，以及函数的最值问题的综合运用。
（1）因为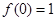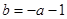，，因此可知f(x)=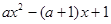，然后利用分类讨论得到不等式的解集。
（2）构造函数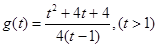，然后利用函数单调性质得到证明 。
(1)f(x)=
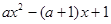
当A.>1时,解为： 1/A.<x<1 当A.=1时，解为空集。
当0<A.<1时,解为： 1<x<1/A.当A.=1时, 解为 x>1
当A.<0时,解为： x>1或x<1/A.。
（2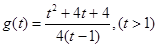） 最小值为3