题目
已知函数
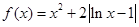 .
.(1)求函数
 的最小值;
的最小值;(2)证明:对任意
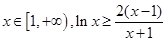 恒成立;
恒成立;(3)对于函数
 图象上的不同两点
图象上的不同两点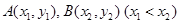 ,如果在函数
,如果在函数 图象上存在点
图象上存在点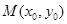 (其中
(其中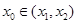 )使得点
)使得点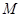 处的切线
处的切线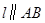 ,则称直线
,则称直线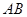 存在“伴侣切线”.特别地,当
存在“伴侣切线”.特别地,当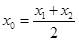 时,又称直线
时,又称直线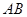 存在 “中值伴侣切线”.试问:当
存在 “中值伴侣切线”.试问:当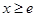 时,对于函数
时,对于函数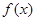 图象上不同两点
图象上不同两点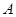 、
、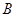 ,直线
,直线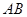 是否存在“中值伴侣切线”?证明你的结论.
是否存在“中值伴侣切线”?证明你的结论.
答案
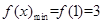 ;(2)见解析;(3)函数f(x)不存在“中值伴侣切线”
;(2)见解析;(3)函数f(x)不存在“中值伴侣切线”
解析
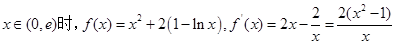


第二问
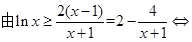
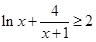
令
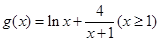
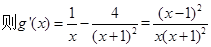 ,
,结合导数来判定。
第三问中,当
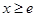 时,
时,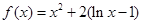 ,
,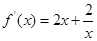 ,假设函数
,假设函数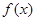 存在“中值伴侣切线”.
存在“中值伴侣切线”. 设
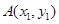 ,
,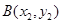 是曲线
是曲线 上的不同两点,且
上的不同两点,且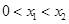
则
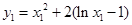 ,
,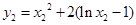 . 故直线AB的斜率:
. 故直线AB的斜率: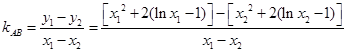

曲线在点
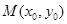 处的切线斜率:
处的切线斜率: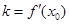
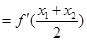 =
=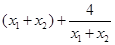
依题意可得。
解:(1)
 …………1分
…………1分
 ……………………………………2分
……………………………………2分
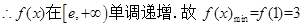 ……………………………4分
……………………………4分(2)
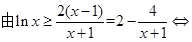
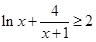
令
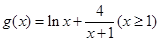
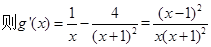 ,………………6分
,………………6分因为
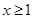 ,显然
,显然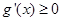 ,所以
,所以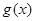 在
在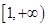 上递增,
上递增,显然有
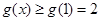 恒成立.(当且仅当x=1时等号成立),即证. ………8分
恒成立.(当且仅当x=1时等号成立),即证. ………8分(3)当
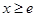 时,
时,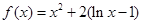 ,
,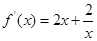 ,假设函数
,假设函数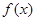 存在“中值伴侣切线”.
存在“中值伴侣切线”. 设
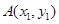 ,
,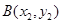 是曲线
是曲线 上的不同两点,且
上的不同两点,且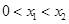
则
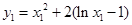 ,
,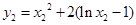 . 故直线AB的斜率:
. 故直线AB的斜率: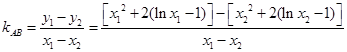
 …………………………………………………………10分
…………………………………………………………10分曲线在点
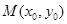 处的切线斜率:
处的切线斜率: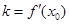
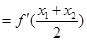 =
=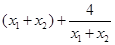 …………………………………………11分
…………………………………………11分依题意得:
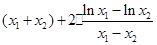
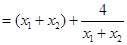
化简可得:
 , 即
, 即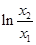 =
=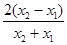
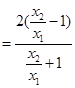 . …………12分
. …………12分 设
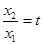 (
(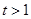 ),上式化为
),上式化为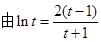 ,由(2)知
,由(2)知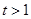 时,
时,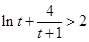 恒成立.
恒成立.所以在
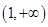 内不存在t,使得
内不存在t,使得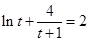 成立.
成立.综上所述,假设不成立.所以,函数f(x)不存在“中值伴侣切线” ………………14分
