题目
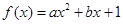 及函数
及函数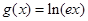 ,函数
,函数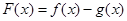 在
在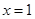 处取得极值.
处取得极值.(Ⅰ)求
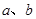 所满足的关系式;
所满足的关系式;(Ⅱ)是否存在实数
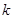 ,使得对(Ⅰ)中任意的实数
,使得对(Ⅰ)中任意的实数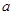 ,直线
,直线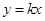 与函数
与函数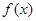 在
在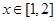 上的图像恒有公共点?若存在,求出
上的图像恒有公共点?若存在,求出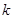 的取值范围,若不存在,请说明理由.
的取值范围,若不存在,请说明理由.
答案
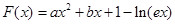 ,
,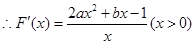 ,
,依题意得:
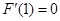 ,即
,即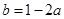 ,……………4分
,……………4分代入得
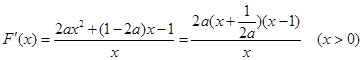
要使
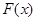 在
在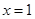 处有极值,则须
处有极值,则须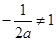 ,即
,即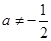 ,
,所以所求
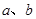 满足的关系式为
满足的关系式为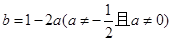 . ……………5分
. ……………5分(Ⅱ)由题意得方程
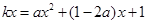 在
在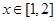 时总有解,所以
时总有解,所以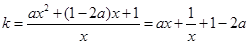 在
在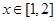 时总有解, ……………6分
时总有解, ……………6分设
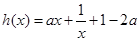 ,则
,则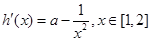 , ……………7分
, ……………7分①当
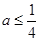 且
且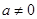 ,
,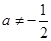 时,
时,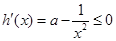 ,
,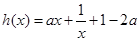 在
在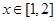 时单调递减,
时单调递减,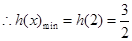 ,
,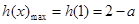 ,
,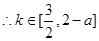 ; …8分
; …8分②当
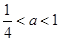 时,令
时,令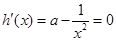 得:
得: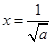 ,
,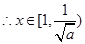 时,
时,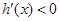 ,
,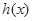 单调递减,
单调递减,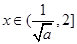 时,
时,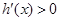 ,
,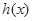 单调递增,
单调递增,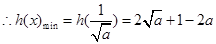 ,
,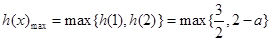 ,
,若
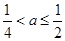 ,则
,则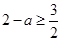 ,
,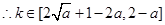 ,
,若
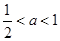 ,则
,则 ,
,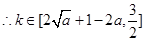 ; ………9分
; ………9分③当
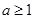 时,
时,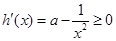 ,
,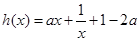 在
在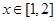 时单调递增,
时单调递增,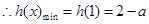 ,
,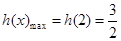 ,
,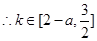 ;……………10分
;……………10分设集合
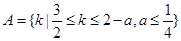 ,
,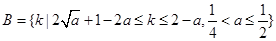 ,
,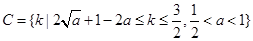 ,
,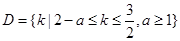 ,
, 所以要使直线
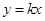 与函数
与函数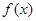 在
在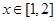 上的图像恒有公共点,则实数
上的图像恒有公共点,则实数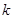 的取值范围为:
的取值范围为: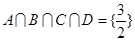 ,所以存在实数
,所以存在实数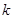 满足题意,其取值范围为
满足题意,其取值范围为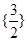 .
.
