题目
 是R上的偶函数.
是R上的偶函数.(1)求a的值;
(2)证明:f(x)在(0,+∞)上是增函数.
答案
 是R上的偶函数,
是R上的偶函数,∴f(x)-f(-x)=0,
∴
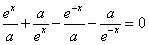 ,即
,即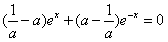 ,
,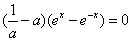 ,
,由于ex-e-x不可能恒为0,
∴当
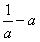 =0时,式子恒成立,
=0时,式子恒成立,又a>0,∴a=1。
(2)证明:∵由(1)知f(x)=ex+
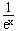 ,在(0,+∞)上任取x1<x2,
,在(0,+∞)上任取x1<x2, 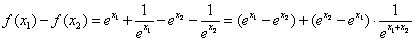 ,
,∵e>1,
∴
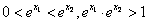 ,
,∴
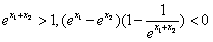 ,
,∴f(x1)-f(x2)<0,即f(x1)<f(x2),
∴f(x)在(0,+∞)上是增函数.
 是R上的偶函数.
是R上的偶函数. 是R上的偶函数,
是R上的偶函数,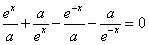 ,即
,即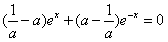 ,
,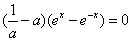 ,
,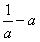 =0时,式子恒成立,
=0时,式子恒成立,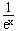 ,在(0,+∞)上任取x1<x2,
,在(0,+∞)上任取x1<x2, 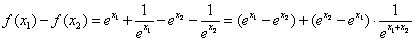 ,
,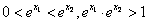 ,
,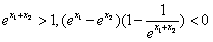 ,
,