题目
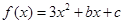 ,不等式
,不等式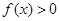 的解集为
的解集为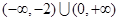 .
.(1)求
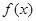 的解析式;
的解析式; (2)若函数
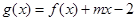 在
在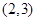 上单调,求实数
上单调,求实数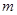 的取值范围;
的取值范围;(3)若对于任意的x∈[-2,2],
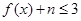 都成立,求实数n的最大值.
都成立,求实数n的最大值.
答案
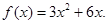 ,(2)
,(2)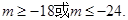 (3)-21.
(3)-21.
解析
试题分析:(1) 根据一元二次方程的根与一元二次不等式的解集关系,可列出两个独立条件,求出解析式. 依题得,
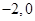 为方程
为方程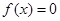 的两个实根,
的两个实根,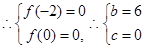
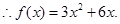
(2)二次函数单调性主要研究对称轴与定义区间相对位置关系,
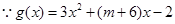 在
在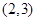 上单调,二次函数开口向上,对称轴
上单调,二次函数开口向上,对称轴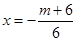
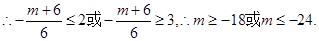 (3)恒成立问题,一般利用变量分离转化为最值问题. 依题得,
(3)恒成立问题,一般利用变量分离转化为最值问题. 依题得, 只要
只要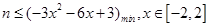 ,设
,设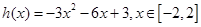
当
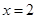 时,
时,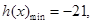
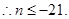 实数n的最大值为
实数n的最大值为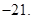
解:(1)依题得,
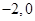 为方程
为方程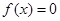 的两个实根,(2分)
的两个实根,(2分)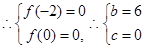 (4分)
(4分)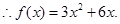 (5分)
(5分)(2)
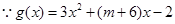 在
在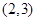 上单调,
上单调,又二次函数开口向上,对称轴
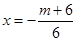 , (7分)
, (7分) (10分)
(10分)(3)依题得,
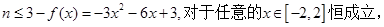 (12分)
(12分)只要
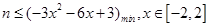 , (13分)
, (13分)设
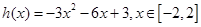
当
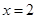 时,
时,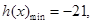 (15分)
(15分)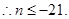 (16分)
(16分)
