题目
| A.(0,2) | B.(0,8) | C.(2,8) | D.(-∞,0) |
答案
解析
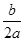 =
=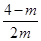 ≥0即0<m≤4时结论显然成立;
≥0即0<m≤4时结论显然成立;当-
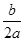 =
=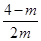 <0时只要Δ=4(4-m)2-8m=4(m-8)(m-2)<0,即4<m<8,则实数m的取值范围是0<m<8,故选B.
<0时只要Δ=4(4-m)2-8m=4(m-8)(m-2)<0,即4<m<8,则实数m的取值范围是0<m<8,故选B.
| A.(0,2) | B.(0,8) | C.(2,8) | D.(-∞,0) |
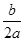 =
=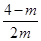 ≥0即0<m≤4时结论显然成立;
≥0即0<m≤4时结论显然成立;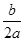 =
=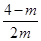 <0时只要Δ=4(4-m)2-8m=4(m-8)(m-2)<0,即4<m<8,则实数m的取值范围是0<m<8,故选B.
<0时只要Δ=4(4-m)2-8m=4(m-8)(m-2)<0,即4<m<8,则实数m的取值范围是0<m<8,故选B.