题目
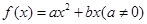 满足条件:①
满足条件:①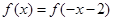 ;②函数
;②函数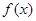 的图像与直线
的图像与直线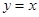 相切.
相切.(1)求函数
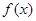 的解析式;
的解析式;(2)若不等式
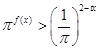 在
在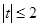 时恒成立,求实数
时恒成立,求实数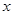 的取值范围.
的取值范围.
答案
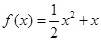 ;(2)
;(2)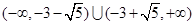 .
.
解析
试题分析:由
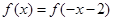
 的图象的对称轴方程是
的图象的对称轴方程是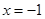 ,于是有
,于是有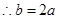 ,依题意,方程组
,依题意,方程组 有且只有一解,利用
有且只有一解,利用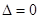 即可求得
即可求得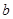 与
与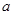 ,从而得函数
,从而得函数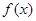 的解析式;(2)利用指数函数的单调性质,知
的解析式;(2)利用指数函数的单调性质,知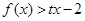 在
在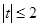 时恒成立,构造函数
时恒成立,构造函数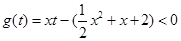 ,由
,由 即可求得答案.
即可求得答案.试题解析:(1)由①可知,二次函数
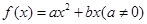 图像对称轴方程是
图像对称轴方程是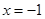 ,
,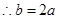 ;
;又因为函数
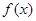 的图像与直线
的图像与直线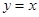 相切,所以方程组
相切,所以方程组 有且只有一解,即方程
有且只有一解,即方程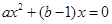 有两个相等的实根,
有两个相等的实根,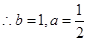 ,
,所以,函数
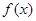 的解析式是
的解析式是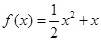 .
.(2)
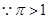 ,
,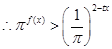 等价于
等价于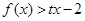 ,
,即不等式
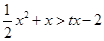 在
在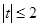 时恒成立,
时恒成立,问题等价于一次函数
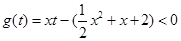 在
在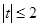 时恒成立,
时恒成立, 即
即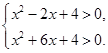 ,
,解得:
 或
或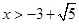 ,
,故所求实数
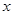 的取值范围是
的取值范围是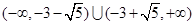 .
.
