题目
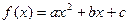 。 (1)若
。 (1)若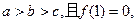 是否存在
是否存在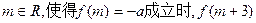 为正数 ,若存在,证明你的结论,若不存在,说明理由;(2)若对
为正数 ,若存在,证明你的结论,若不存在,说明理由;(2)若对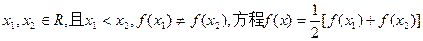 有2个不等实根,证明必有一个根属于
有2个不等实根,证明必有一个根属于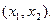 (3)若
(3)若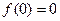 ,是否存在
,是否存在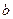 的值使
的值使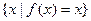 =
=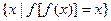 成立,若存在,求出
成立,若存在,求出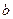 的取值范围,若不存在,说明理由。
的取值范围,若不存在,说明理由。
答案
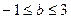
解析
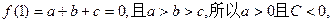
∵

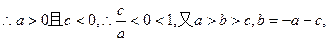 ∴可得
∴可得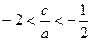 ,
,假设存在,由题意,则
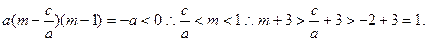
因为
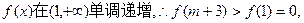
即 存在这样的
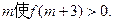
(2)令
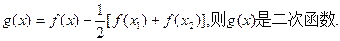
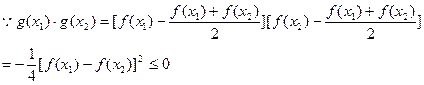
又
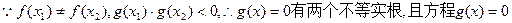
的根必有一个属于
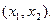
(3)由
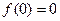 得
得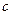 =0,∴
=0,∴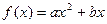
由
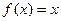 ,得方程
,得方程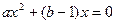 ,解得:
,解得: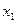 =0,
=0,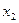 =
=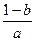 ,
,又由
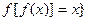 得:
得: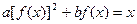
∴
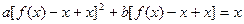
∴
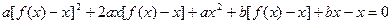
∴
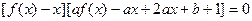
即
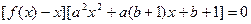
∴
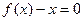 或
或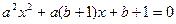 (*)
(*)由题意(*)式的解为0或
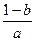 或无解,
或无解,当(*)式的解为0时,可解得
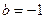 ,经检验符合题意;
,经检验符合题意;当(*)式的解为
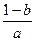 时,可解得
时,可解得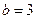 ,经检验符合题意;
,经检验符合题意;当(*)式无解时,
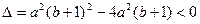 ,即
,即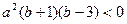
∴
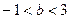 综上可知,当
综上可知,当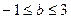 时满足题意。
时满足题意。
