题目

已知二次函数f(x)=ax²+bx+c和一次函数g(x)=－bx，其中a、b、c满足a>b>c,a+b+c=0,(a,b,c∈R).
(1)求证：两函数的图象交于不同的两点A、B；
(2)求线段AB在x轴上的射影A₁B₁的长的取值范围.

答案

答案见解析

解析

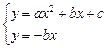(1)证明：由消去y得ax²+2bx+c=0
Δ=4b²－4ac=4(－a－c)²－4ac=4(a²+ac+c²)=4［(a+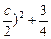c²］
∵a+b+c=0,a>b>c,∴a>0,c<0
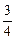∴c²>0,∴Δ>0,即两函数的图象交于不同的两点.
(2)解：设方程ax²+bx+c=0的两根为x₁和x₂,则x₁+x₂=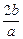－,x₁x₂=.
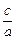|A₁B₁|²=(x₁－x₂)²=(x₁+x₂)²－4x₁x₂

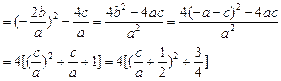
∵a>b>c,a+b+c=0,a>0,c<0
∴a>－a－c>c,解得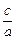∈(－2,－)
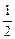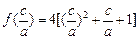∵的对称轴方程是.
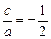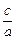∈(－2,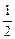－)时，为减函数
∴|A₁B₁|²∈(3,12),故|A₁B₁|∈().
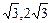