题目
A.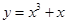
|
B.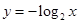
|
C.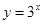
|
D.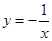
|
答案
解析
A:y=x3+x,f(﹣x)=(﹣x)3+(﹣x)=﹣x3﹣x=﹣f(x)是奇函数,且由幂函数的性质可知函数在R上单调递增本题主要考查了函数的奇偶性及函数的单调性的判断,尤其y=﹣
 的单调区间的求解是解答中容易出现错误的地方,要注意掌握.
的单调区间的求解是解答中容易出现错误的地方,要注意掌握.B:y=﹣log2x的定义域(0,+∞)关于原点不对称,不是奇函数;D:y=3x不是奇函数; A:y=﹣
 在(,+∞),(﹣∞,0)上单调递增,但是在整个定义域内不是单调递增函数;
在(,+∞),(﹣∞,0)上单调递增,但是在整个定义域内不是单调递增函数;解:
A:y=x3+x,f(﹣x)=(﹣x)3+(﹣x)=﹣x3﹣x=﹣f(x)是奇函数,且由幂函数的性质可知函数在R上单调递增,故A正确
故选A
B:y=﹣log2x的定义域(0,+∞)关于原点不对称,不是奇函数,故B错误
C:y=3x不是奇函数,故C错误
D:y=﹣
 在(,+∞),(﹣∞,0)上单调递增,但是在整个定义域内不是单调递增函数,故D错误
在(,+∞),(﹣∞,0)上单调递增,但是在整个定义域内不是单调递增函数,故D错误
