题目
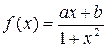 是定义在
是定义在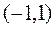 上的奇函数,且
上的奇函数,且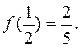
(1)确定函数
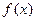 的解析式;
的解析式;(2)判断并证明
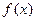 在
在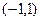 的单调性;
的单调性;(3)解不等式
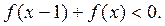
答案
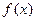 是奇函数
是奇函数∴
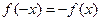
∴
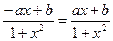 得
得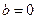 ……..2
……..2又
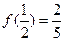 ,代入函数得
,代入函数得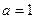 .
.∴
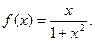 …….2
…….2(2)在
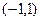 上任取两个值
上任取两个值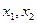 ,且
,且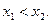
则
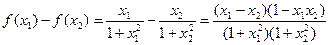
∵
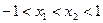 ∴
∴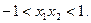
∴
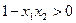
又
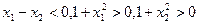
∴
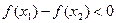 ,∴
,∴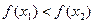
∴
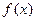 在
在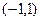 上是增函数………..8
上是增函数………..8(3)由已知得
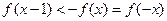 ……….9
……….9∴
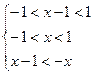 ∴
∴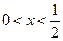 .……………………12分
.……………………12分
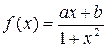 是定义在
是定义在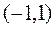 上的奇函数,且
上的奇函数,且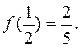
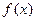 的解析式;
的解析式;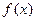 在
在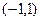 的单调性;
的单调性;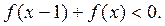
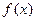 是奇函数
是奇函数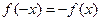
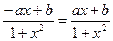 得
得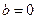 ……..2
……..2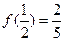 ,代入函数得
,代入函数得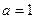 .
.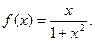 …….2
…….2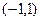 上任取两个值
上任取两个值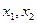 ,且
,且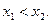
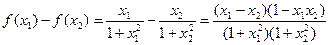
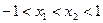 ∴
∴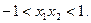
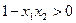
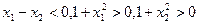
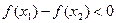 ,∴
,∴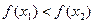
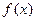 在
在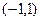 上是增函数………..8
上是增函数………..8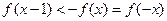 ……….9
……….9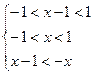 ∴
∴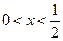 .……………………12分
.……………………12分