题目
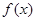 在定义域R上不是常数函数,且
在定义域R上不是常数函数,且 满足条件:对任意
满足条件:对任意 R,
R,都有
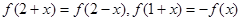 ,则
,则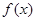 是
是| A.奇函数但非偶函数 | B.偶函数但非奇函数 |
| C.既是奇函数又是偶函数 | D.是非奇非偶函数 |
答案
解析
解答:解:∵对任意x∈R,都有f(2+x)=f(2-x),f(1+x)=-f(x)
∴f(2+x)=f[1+(1+x)]=-f(1+x)=f(x),f(2-x)=f[1+(1-x)]=-f(1-x)=f(-x)
∴f(x)=f(-x)
故f(x)为偶函数
又∵既是奇函数又是偶函数只有常数函数,函数f(x)在定义域R上不是常数函数
∴函数f(x)不可能为奇函数
故选B
