题目

设函数f（x）=lnx-px+1，其中p为常数．
（Ⅰ）求函数f（x）的极值点；
（Ⅱ）当p＞0时，若对任意的x＞0，恒有在f（x）≤0，求p的取值范围；
（Ⅲ）求证：

ln22

22

+

ln32

32

+…+

lnn2

n2

＜

2n2-n-1

2(n+1)

(n∈N，n≥2)．

答案

（Ⅰ）∵f（x）=lnx-px+1定义域为（0，+∞），
∴f′(x)=

1

x

-p=

1-px

x

，
当p≤0时，f′（x）＞0，f（x）在（0，+∞）上无极值点
当p＞0时，令f"（x）=0，∴x=

1

p

∈（0，+∞），f"（x）、f（x）随x的变化情况如下表：



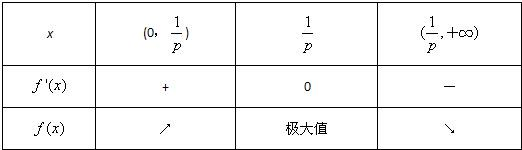
从上表可以看出：当p＞0时，f（x）有唯一的极大值点x=

1

p

（Ⅱ）当p＞0时，在x=

1

p

处取得极大值f(

1

p

)=ln

1

p

，此极大值也是最大值，
要使f（x）≤0恒成立，只需f(

1

p

)=ln

1

p

≤0，
∴p≥1
∴p的取值范围为[1，+∞）
（Ⅲ）令p=1，由（Ⅱ）知，lnx-x+1≤0，
∴lnx≤x-1，
∵n∈N，n≥2
∴lnn²≤n²-1，
∴

lnn2

n2

≤

n2-1

n2

=1-

1

n2

∴

ln22

22

+

ln32

32

++

lnn2

n2

≤(1-

1

22

)+(1-

1

32

)++(1-

1

n2

)=(n-1)-(

1

22

+

1

32

++

1

n2

)＜(n-1)-(

1

2×3

+

1

3×4

++

1

n(n+1)

)=(n-1)-(

1

2

-

1

3

+

1

3

-

1

4

++

1

n

-

1

n+1

)
=(n-1)-(

1

2

-

1

n+1

)=

2n2-n-1

2(n+1)

∴结论成立

解析