题目
f(cos2θ﹣7)+f(4m﹣2mcosθ)>f(0),对一切
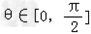 都成立?若存在,求出实数m的取值范围;若不存在,请说明理由.
都成立?若存在,求出实数m的取值范围;若不存在,请说明理由.答案
∴f(0)=0
∵f(cos2θ﹣7)+f(4m﹣2mcosθ)>f(0)
∴f(cos2θ﹣7)>f(2mcosθ﹣4m)恒成立
又∵f(x)在R上单调递增
∴cos2θ﹣7>2mcosθ﹣4m
∴2cos2θ﹣8>2mcosθ﹣4m 即cosθ+2>m恒成立
∵0≤cosθ≤1
∴2≤2+cosθ≤3
∴m<2
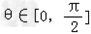 都成立?若存在,求出实数m的取值范围;若不存在,请说明理由.
都成立?若存在,求出实数m的取值范围;若不存在,请说明理由.