题目

已知定义在R的函数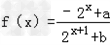（a，b为实常数）．
（1）当a=b=1时，证明：f（x）不是奇函数；
（2）设f（x）是奇函数，求a与b的值；
（3）当f（x）是奇函数时，证明对任何实数x、c都有f（x）＜c²﹣3c+3成立．

答案

解：（1），
，
，
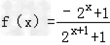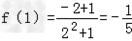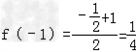所以f（﹣1）≠﹣f（1），f（x）不是奇函数；
（2）f（x）是奇函数时，f（﹣x）=﹣f（x），
即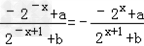对任意x∈R恒成立．
化简整理得（2a﹣b）²2^x+（2ab﹣4）2^x+（2a﹣b）=0对任意x∈R恒成立．
∴，
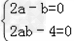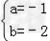∴（舍）或，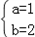
∴．
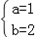（3）由（2）得：，
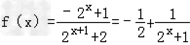∵2^x＞0，
∴2^x+1＞1，
∴，
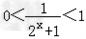从而；
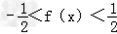而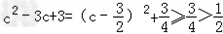对任何实数c成立；
所以对任何实数x、c都有f（x）＜c²﹣3c+3成立．

解析