题目
(1)判断函数的奇偶性;
(2)判断f(x)的单调性并证明。
答案
(1)解:由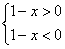 ,解得:
,解得: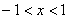 ,
,
∴f(x)的定义域为(-1,1),关于原点对称,
又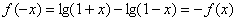 ,
,
∴f(x)是奇函数。
(2)解:在定义域上,f(x)是减函数;
证明:设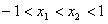 ,
,
则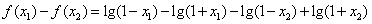
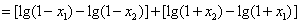 ,
,
∵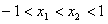 ,
,
∴ ,
,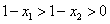 ,
,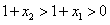 ,
,
∴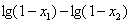 >0 ,
>0 ,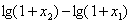 >0,
>0,
∴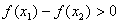 , 即
, 即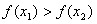 ,
,
∴在(-1,1)上,f(x)是减函数。
(1)解:由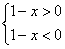 ,解得:
,解得: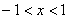 ,
,
∴f(x)的定义域为(-1,1),关于原点对称,
又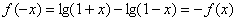 ,
,
∴f(x)是奇函数。
(2)解:在定义域上,f(x)是减函数;
证明:设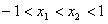 ,
,
则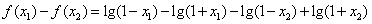
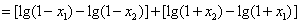 ,
,
∵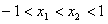 ,
,
∴ ,
,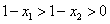 ,
,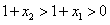 ,
,
∴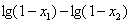 >0 ,
>0 ,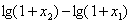 >0,
>0,
∴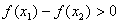 , 即
, 即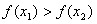 ,
,
∴在(-1,1)上,f(x)是减函数。