题目
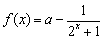 。
。(1)求证:不论a为何实数f(x)总是为增函数;
(2)确定a的值,使f(x)为奇函数;
(3)当f(x)为奇函数时,求f(x)的值域。
答案
(1)证明:∵f(x)的定义域为R,设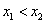 ,
,
则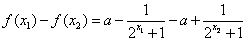 =
=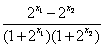 ,
,
∵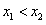 ,
,
∴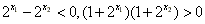 ,
,
∴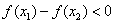 ,即
,即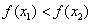 ,
,
所以不论a为何实数f(x)总为增函数。
(2)解:∵f(x)为奇函数,
∴f(-x)=-f(x),即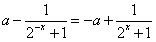 ,
,
解得: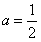 ,
,
∴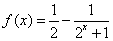 。
。
(3)解:由(2)知,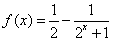 ,
,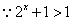 ,
,
∴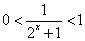 ,∴
,∴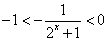 ,
,
∴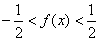 ,
,
所以,f(x)的值域为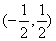 。
。
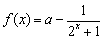 。
。(1)证明:∵f(x)的定义域为R,设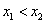 ,
,
则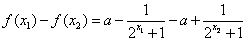 =
=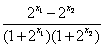 ,
,
∵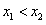 ,
,
∴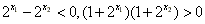 ,
,
∴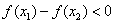 ,即
,即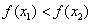 ,
,
所以不论a为何实数f(x)总为增函数。
(2)解:∵f(x)为奇函数,
∴f(-x)=-f(x),即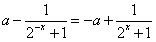 ,
,
解得: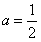 ,
,
∴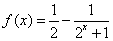 。
。
(3)解:由(2)知,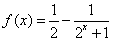 ,
,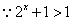 ,
,
∴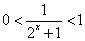 ,∴
,∴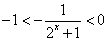 ,
,
∴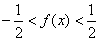 ,
,
所以,f(x)的值域为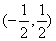 。
。