题目
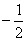 ),当x∈(-4,-2)时,f(x)的最大值为-4.
),当x∈(-4,-2)时,f(x)的最大值为-4.(Ⅰ)求实数a的值;
(Ⅱ)设b≠0,函数
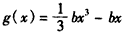 ,x∈(1,2),若对任意的x1∈(1,2),总存在x2∈(1,2),使f(x1)-g(x2)=0,求实数b的取值范围.
,x∈(1,2),若对任意的x1∈(1,2),总存在x2∈(1,2),使f(x1)-g(x2)=0,求实数b的取值范围. 答案
解:(Ⅰ)由已知,得2f(x+2)=-f(-x),
∵f(x)是奇函数,
∴f(x)=-f(-x),
∴2f(x+2)=f(x),
∴f(x)=2f(x+2)=4f(x+4),
∵x∈(0,2)时,f(x)=1nx+ax,设x∈(-4,-2),则x+4∈(0,2),
∴f(x+4)=ln(x+4)+a(x+4),
∴x∈(-4,-2)时,f(x)=4f(x+4)=4ln(x+4)+4a(x+4),
所以,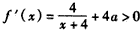 ,
,
∵x∈(-4,-2),∴-4ax<4+16a,
∵ ,∴
,∴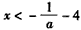 ,
,
又由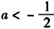 ,可得
,可得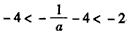 ,
,
∴f(x)在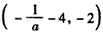 上是增函数,在
上是增函数,在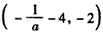 上是减函数,
上是减函数,
∴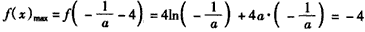 ,
,
∴ a=-l。
(Ⅱ)设f(x)的值域为A,g(x)的值域为B,则由已知,对于任意的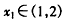 ,总存在
,总存在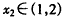 ,
,
使得 得
得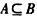 ,
,
由(Ⅰ)知,a=-1,
当x∈(1,2)时,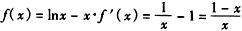 ,
,
∵x∈(1,2),
∴f"(x)<0,f(x)在x∈(1,2)上单调递减函数,
∴f(x)的值域为A=(ln2-2,-1),
∵g"(x)=bx2-b=b(x-1)(x+1),
∴(1)当b<0时,g(x)在(1,2)上是减函数,
此时,g(x)的值域为 ,
,
为满足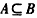 ,又
,又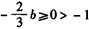 ,∴
,∴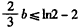 ,即
,即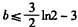 。
。
(2)当b>0时,g(x)在(1,2)上是递增函数,
此时g(x)的值域为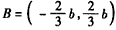 ,
,
为满足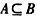 ,又
,又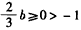 ,则
,则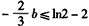 ,
,
∴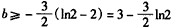 。
。
综上可知,b的取值范围是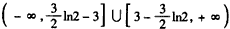 。
。
