题目

如图，在△ABC中，AB=

2

3

AC，D、E分别为边AB、AC的中点，CD与BE相交于点P，
（1）若AB=2，四边形ADPE的面积记为S（A），试用角A表示出S（A），并求S的最大值；
（2）若

BE

CD

＜t恒成立，求t的最小值．

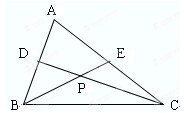
答案

（1）∵点P是△ABC的重心，


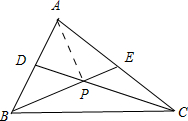
∴S=S_△APD+S_△AEP=

1

3

S△ABC=

1

6

AB•AC•sinA=

1

6

×2×3×sinA=sinA．
当A=

π

2

时，S取得最大值1．
（2）设AB=2x，AC=3x，

BE2

CD2

=

4x2+ 9x2 4 -2×2x× 3x 2 cosA

9x2+x2-2×x×3x×cosA

=

25-24cosA

40-24cosA

=1-

15

40-24cosA

，
∵A∈（0，π），∴cosA∈（-1，1），可得

1

4

＜

BE

CD

＜

7

8

，
若

BE

CD

＜t恒成立，则t≥

7

8

，
∴t的最小值为

7

8

．

解析