题目
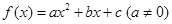 满足
满足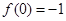 ,对任意
,对任意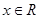 都有
都有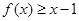 ,且
,且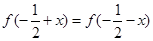 .
.(1)求函数
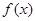 的解析式;
的解析式;(2)是否存在实数
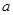 ,使函数
,使函数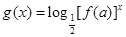 在
在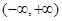 上为减函数?若存在,求出实数
上为减函数?若存在,求出实数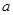 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
答案
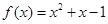 ;(2)存在实数
;(2)存在实数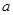 ,
,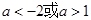 .
.
解析
试题分析:(1)根据
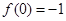 求得
求得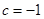 ;
;根据对任意
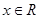 ,有
,有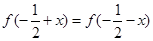 ,确定
,确定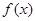 图像的对称轴为直线
图像的对称轴为直线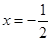 ,求得
,求得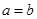 ;
;利用对任意
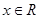 都有
都有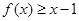 ,转化成
,转化成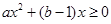 对任意
对任意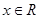 成立,解得
成立,解得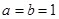 .
.(2)化简函数
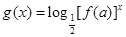
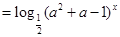 ,其定义域为
,其定义域为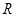 ,
,令
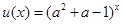 ,利用复合函数的单调性,得到
,利用复合函数的单调性,得到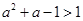 求解,得
求解,得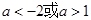 ,肯定存在性.
,肯定存在性.试题解析:
(1)由
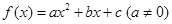 及
及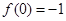 ∴
∴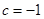 1分
1分又对任意
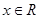 ,有
,有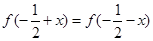
∴
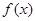 图像的对称轴为直线
图像的对称轴为直线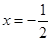 ,则
,则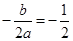 ,∴
,∴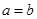 3分
3分又对任意
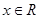 都有
都有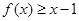 ,
,即
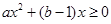 对任意
对任意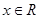 成立,
成立,∴
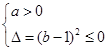 ,故
,故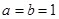 6分
6分∴
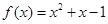 7分
7分(2)由(1)知
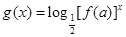
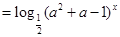 ,其定义域为
,其定义域为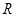 8分
8分令
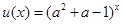
要使函数
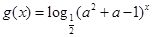 在
在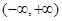 上为减函数,
上为减函数,只需函数
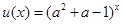 在
在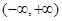 上为增函数, 11分
上为增函数, 11分由指数函数的单调性,有
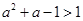 ,解得
,解得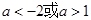 13分
13分故存在实数
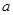 ,当
,当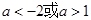 时,函数
时,函数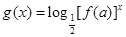 在
在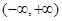 上为减函数 14分
上为减函数 14分
