题目
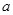 为实数,函数
为实数,函数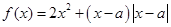 .
.(Ⅰ)若
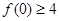 ,求
,求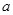 的取值范围;
的取值范围;(Ⅱ)求函数
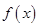 的最小值.
的最小值.
答案
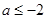 ;(Ⅱ)
;(Ⅱ)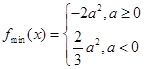 .
.
解析
试题分析:(Ⅰ)由条件代入可解得
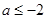 ;(Ⅱ)结合一元二次函数的最值以及分段函数可以求得函数
;(Ⅱ)结合一元二次函数的最值以及分段函数可以求得函数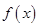 的最小值,详解如下;
的最小值,详解如下;试题解析:(Ⅰ)因为
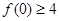 ,
,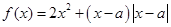 ,所以
,所以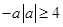 ,可知
,可知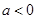 ,得到
,得到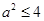 ,所以
,所以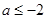 ;
;(Ⅱ)将函数
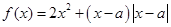 去掉绝对值,化简有:
去掉绝对值,化简有: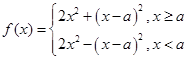 .
.令
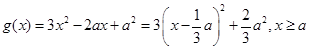 ;
;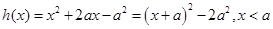 .
.当
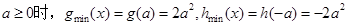 ,所以
,所以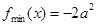 ;
;当
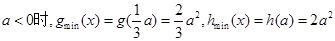 ,所以
,所以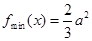 .
.综上,函数
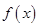 的最小值为:
的最小值为: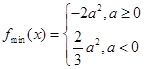 .
.
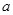 为实数,函数
为实数,函数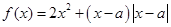 .
.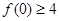 ,求
,求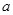 的取值范围;
的取值范围;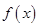 的最小值.
的最小值.
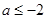 ;(Ⅱ)
;(Ⅱ)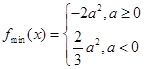 .
.
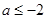 ;(Ⅱ)结合一元二次函数的最值以及分段函数可以求得函数
;(Ⅱ)结合一元二次函数的最值以及分段函数可以求得函数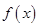 的最小值,详解如下;
的最小值,详解如下;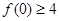 ,
,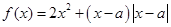 ,所以
,所以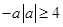 ,可知
,可知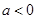 ,得到
,得到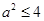 ,所以
,所以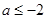 ;
;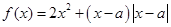 去掉绝对值,化简有:
去掉绝对值,化简有: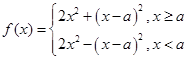 .
.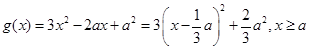 ;
;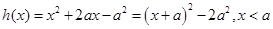 .
.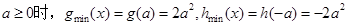 ,所以
,所以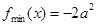 ;
;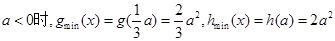 ,所以
,所以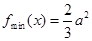 .
.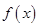 的最小值为:
的最小值为: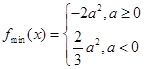 .
.