题目
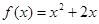 .
.(Ⅰ)若
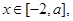 求
求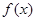 的值域;
的值域;(Ⅱ)若存在实数
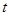 ,当
,当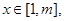
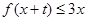 恒成立,求实数
恒成立,求实数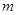 的取值范围.
的取值范围.
答案
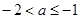 时,
时, 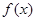 的值域为:
的值域为: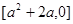 .当
.当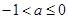 时,
时,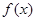 的值域为:
的值域为: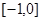 .当
.当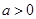 时,
时,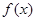 的值域为:
的值域为: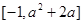 .(II)
.(II)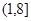 .
.
解析
试题分析:(I)由于
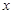 的范围含有参数
的范围含有参数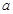 ,故结合抛物线的图象对
,故结合抛物线的图象对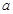 分情况进行讨论.
分情况进行讨论. (II)由
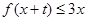 恒成立得:
恒成立得: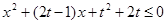 恒成立,
恒成立,令
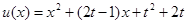 ,
,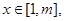 则只需
则只需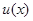 的最大值小于等于0.
的最大值小于等于0.由此得:
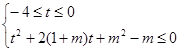 ,令
,令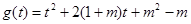
则原题可转化为:存在
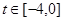 ,使得
,使得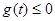 .这又需要
.这又需要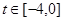 时
时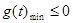 .接下来又对二次函数
.接下来又对二次函数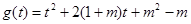 分情况讨论,从而求出实数
分情况讨论,从而求出实数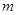 的取值范围.
的取值范围.试题解析:(I)由题意得:
当
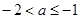 时,
时,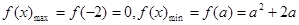 ,
,∴此时
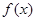 的值域为:
的值域为: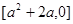 2分
2分当
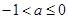 时,
时,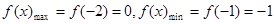 ,
,∴此时
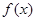 的值域为:
的值域为: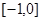 4分
4分当
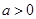 时,
时,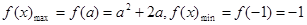 ,
,∴此时
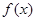 的值域为:
的值域为: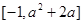 6分
6分(II)由
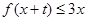 恒成立得:
恒成立得: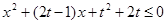 恒成立,
恒成立,令
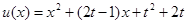 ,
,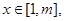 因为抛物线的开口向上,所以
因为抛物线的开口向上,所以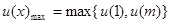 ,由
,由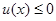 恒成立知:
恒成立知: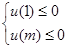 8分
8分化简得:
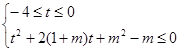 令
令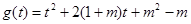
则原题可转化为:存在
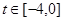 ,使得
,使得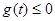 即:当
即:当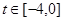 ,
,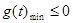 10分
10分∵
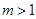 ,
,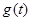 的对称轴:
的对称轴: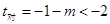
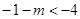 即:
即: 时,
时,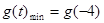
∴

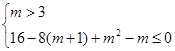 解得:
解得: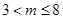
②当
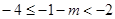 即:
即: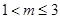 时,
时,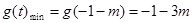
∴

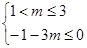 解得:
解得: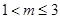
综上:
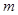 的取值范围为:
的取值范围为: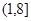 13分
13分法二:也可
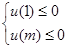 ,
,化简得:
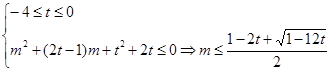 有解.
有解.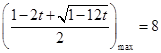 ,则
,则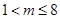 .
.
