题目
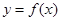 在区间
在区间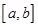 上存在
上存在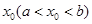 ,满足
,满足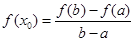 ,则称
,则称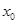 是函数
是函数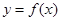 在区间
在区间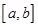 上的一个均值点。已知函数
上的一个均值点。已知函数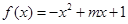 在区间
在区间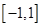 上存在均值点,则实数
上存在均值点,则实数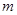 的取值范围是 .
的取值范围是 .
答案
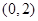 .
.
解析
试题分析:由题意设函数
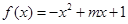 在区间
在区间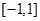 上的均值点为
上的均值点为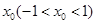 ,则
,则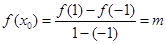 ,易知函数
,易知函数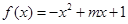 的对称轴为
的对称轴为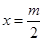 ,①当
,①当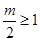 即
即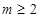 时,有
时,有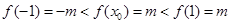 ,显然不成立,不合题意;②当
,显然不成立,不合题意;②当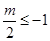 即
即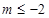 时,有
时,有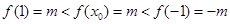 ,显然不成立,不合题意;③当
,显然不成立,不合题意;③当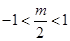 即
即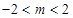 时,(1)当
时,(1)当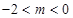 有
有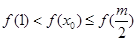 ,即
,即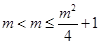 ,显然不成立;(2)当
,显然不成立;(2)当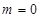 时,
时, 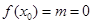 ,此时
,此时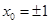 ,与
,与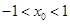 矛盾,即
矛盾,即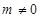 ;(3)当
;(3)当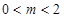 时,有
时,有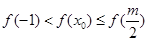 ,即
,即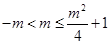 ,解得
,解得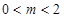 ,综上所述得实数
,综上所述得实数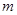 的取值范围为
的取值范围为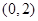 .
.
