题目
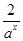 (a>0,a≠1)
(a>0,a≠1)(1)若a>1,且关于x的方程f(x)=m有两个不同的正数解,求实数m的取值范围;
(2)设函数g(x)=" f(" x),x∈[ 2,+∞),
 满足如下性质:若存在最大(小)值,则最大(小)值与a无关.试求a的取值范围.
满足如下性质:若存在最大(小)值,则最大(小)值与a无关.试求a的取值范围.
答案
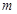 的取值范围为区间
的取值范围为区间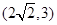 ;(2)实数a的取值范围是
;(2)实数a的取值范围是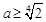 .
.
解析
试题分析:(1)令
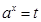 ,换元将问题转化为关于
,换元将问题转化为关于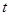 的方程
的方程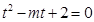 有相异的且均大于1的两根,利用二次函数的性质解答即可;(2)算得
有相异的且均大于1的两根,利用二次函数的性质解答即可;(2)算得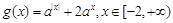 ,分类讨论①当
,分类讨论①当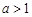 ,②当
,②当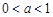 ,再分
,再分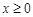 ,
,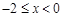 讨论解答.
讨论解答.试题解析:(1)令
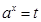 ,
,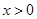 ,因为
,因为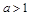 ,所以
,所以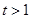 ,所以关于
,所以关于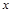 的方程
的方程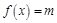 有两个不同的正数解等价于关于
有两个不同的正数解等价于关于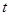 的方程
的方程 有相异的且均大于1的两根,即关于
有相异的且均大于1的两根,即关于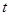 的方程
的方程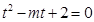 有相异的且均大于1的两根, 2分
有相异的且均大于1的两根, 2分所以
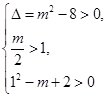 , 4分
, 4分解得
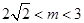 ,故实数
,故实数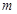 的取值范围为区间
的取值范围为区间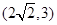 . 6分
. 6分(2)
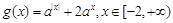
①当
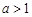 时,
时,a)
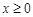 时,
时,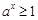 ,
,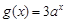 ,所以
,所以 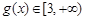 ,
, b)
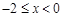 时,
时,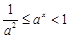
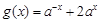 ,所以
,所以 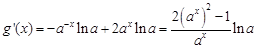 8分
8分ⅰ)当
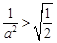 即
即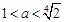 时,对
时,对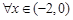 ,
,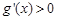 ,所以
,所以 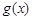 在
在 上递增,
上递增,所以
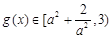 ,综合a) b)
,综合a) b)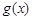 有最小值为
有最小值为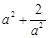 与a有关,不符合 10分
与a有关,不符合 10分ⅱ)当
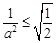 即
即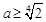 时,由
时,由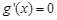 得
得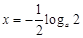 ,且当
,且当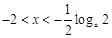 时,
时, ,当
,当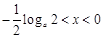 时,
时,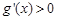 ,所以
,所以 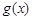 在
在 上递减,在
上递减,在 上递增,所以
上递增,所以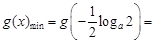
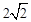 ,综合a) b)
,综合a) b) 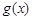 有最小值为
有最小值为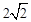 与a无关,符合要求. 12分
与a无关,符合要求. 12分②当
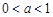 时,
时,a)
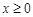 时,
时,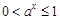 ,
,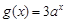 ,所以
,所以 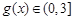
b)
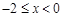 时,
时,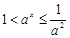 ,
,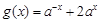 ,
,所以

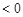 ,
,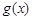 在
在 上递减,
上递减,所以
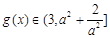 ,综合a) b)
,综合a) b) 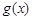 有最大值为
有最大值为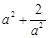 与a有关,不符合 15分
与a有关,不符合 15分综上所述,实数a的取值范围是
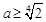 . 16分
. 16分
