题目
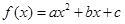 ,满足
,满足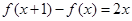 ,且
,且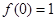 ,若在区间
,若在区间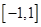 上,不等式
上,不等式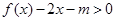 恒成立,则实数m的取值范围为 .
恒成立,则实数m的取值范围为 .
答案
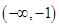
解析
试题分析:由
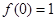 可知
可知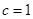 ,那么
,那么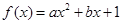 ,所以由
,所以由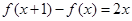 ,化简整理得:
,化简整理得: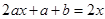 ,所以有
,所以有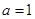 ,
,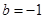 ,所以二次函数的解析式为:
,所以二次函数的解析式为: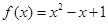 .由已知得在区间
.由已知得在区间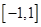 上,不等式
上,不等式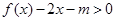 恒成立,即
恒成立,即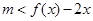 恒成立,只要
恒成立,只要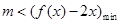 即可.又
即可.又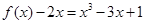
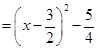 ,对称轴是
,对称轴是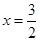 ,开口向上,所以函数
,开口向上,所以函数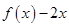 在区间
在区间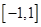 是单调递减的,所以函数
是单调递减的,所以函数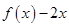 在区间
在区间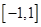 上的最小值是:
上的最小值是: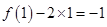 ,所以
,所以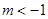 .
.
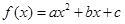 ,满足
,满足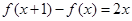 ,且
,且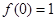 ,若在区间
,若在区间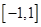 上,不等式
上,不等式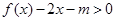 恒成立,则实数m的取值范围为 .
恒成立,则实数m的取值范围为 .
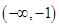
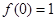 可知
可知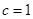 ,那么
,那么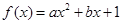 ,所以由
,所以由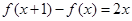 ,化简整理得:
,化简整理得: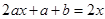 ,所以有
,所以有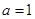 ,
,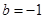 ,所以二次函数的解析式为:
,所以二次函数的解析式为: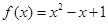 .由已知得在区间
.由已知得在区间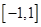 上,不等式
上,不等式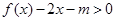 恒成立,即
恒成立,即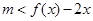 恒成立,只要
恒成立,只要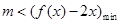 即可.又
即可.又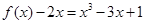
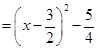 ,对称轴是
,对称轴是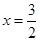 ,开口向上,所以函数
,开口向上,所以函数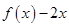 在区间
在区间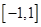 是单调递减的,所以函数
是单调递减的,所以函数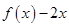 在区间
在区间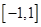 上的最小值是:
上的最小值是: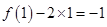 ,所以
,所以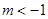 .
.