题目
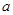 为实数,记函数
为实数,记函数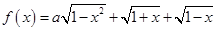 的最大值为
的最大值为 .
.(1)设
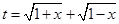 ,求
,求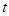 的取值范围,并把
的取值范围,并把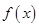 表示为
表示为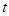 的函数
的函数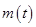 ;
;(2)求
 .
.
答案
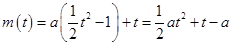
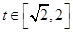 ;(Ⅱ)
;(Ⅱ)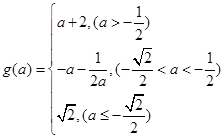
解析
试题分析:观察到
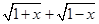 与
与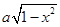 是有关联的,平方后就可以看出彼此之间的关联.这样
是有关联的,平方后就可以看出彼此之间的关联.这样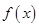 就可以化成以t为自变量的函数.那么第二问就转化成了带参数的二次函数的最值问题.根据对称轴进行分类讨论即可.
就可以化成以t为自变量的函数.那么第二问就转化成了带参数的二次函数的最值问题.根据对称轴进行分类讨论即可.试题解析:(1)因为
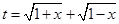 ,
,所以要使
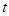 有意义,必须
有意义,必须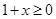 且
且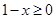 ,即
,即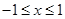
因为
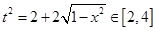 ,且
,且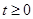 ①
①所以
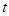 得取值范围是
得取值范围是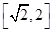
由①得
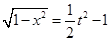
所以
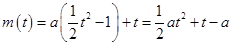 ,
,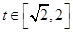 ; 2分
; 2分(2)由题意知
 即为函数
即为函数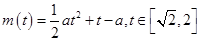 的最大值.
的最大值.因为直线
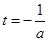 是抛物线
是抛物线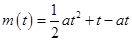 的对称轴,
的对称轴,所以可分以下几种情况进行讨论:
当
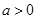 时函数
时函数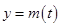 ,
,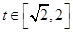 的图像是开口向上的抛物线的一段,
的图像是开口向上的抛物线的一段,由
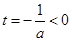 知
知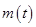 在
在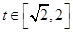 上单调递增,故
上单调递增,故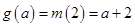 ; 4分
; 4分②当
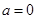 时,
时,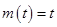 ,
,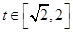 ,有
,有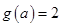 ; 6分
; 6分③当
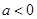 时,函数
时,函数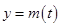 ,
,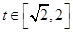 的图像是开口向下的抛物线的一段,
的图像是开口向下的抛物线的一段,若
 ,即
,即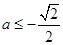 时,
时,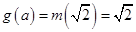 ,
,若
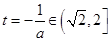 ,即
,即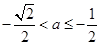 时,
时,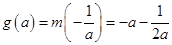 ,
,若
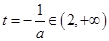 ,即
,即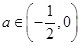 时,
时,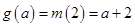 9分
9分综上,有
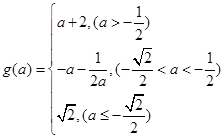 10分
10分
