题目
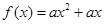 和
和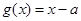 .其中
.其中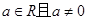 .
.(1)若函数
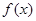 与
与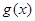 的图像的一个公共点恰好在
的图像的一个公共点恰好在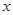 轴上,求
轴上,求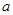 的值;
的值;(2)若
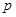 和
和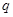 是方程
是方程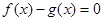 的两根,且满足
的两根,且满足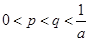 ,证明:当
,证明:当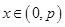 时,
时,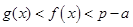 .
.
答案
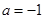 ;(2)证明过程详见解析.
;(2)证明过程详见解析.
解析
试题分析:本题考查一次函数与二次函数图像的关系以及作差法比较大小证明不等式问题,考查学生分析问题解决问题的能力.第一问,先求
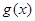 与
与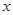 轴的交点,由已知得此交点同时也在
轴的交点,由已知得此交点同时也在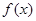 图像上,所以代入到
图像上,所以代入到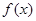 解析式中,解出
解析式中,解出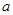 的值;第二问,作差法比较
的值;第二问,作差法比较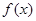 与
与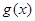 的大小,再用作差法比较
的大小,再用作差法比较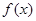 与
与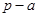 的大小.
的大小.试题解析:(1)设函数
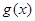 图象与
图象与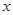 轴的交点坐标为
轴的交点坐标为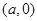 ,
,又∵点
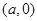 也在函数
也在函数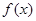 的图象上,∴
的图象上,∴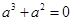 .
.而
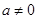 ,∴
,∴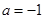 .(4分)
.(4分)(2)由题意可知
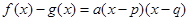 .
.∵
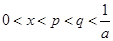 ,∴
,∴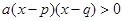 ,
,∴当
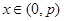 时,
时,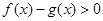 ,即
,即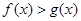 .(8分)
.(8分)又
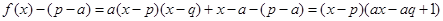 ,
,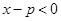 ,且
,且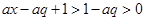 ,∴
,∴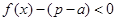 ,∴
,∴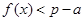 ,
,综上可知,
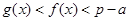 .(13分)
.(13分)
