题目
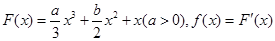 ,若
,若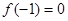 且对任意实数
且对任意实数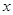 均有
均有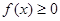 成立.
成立.(1)求
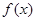 表达式;
表达式;(2)当
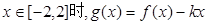 是单调函数,求实数
是单调函数,求实数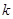 的取值范围.
的取值范围.
答案
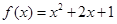 ;(2)
;(2)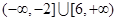 .
.
解析
试题分析:本题考查导数的运算以及二次函数的判别式、单调性等基础知识,考查运算能力和分析问题解决问题的能力,考查数形结合思想.第一问,对
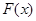 求导得到
求导得到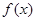 解析式,因为
解析式,因为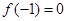 ,所以得到
,所以得到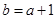 ,又因为
,又因为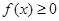 恒成立,所以
恒成立,所以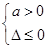 ,两式联立解出
,两式联立解出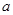 和
和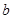 ,从而确定
,从而确定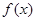 解析式;第二问,先利用第一问的结论,得到
解析式;第二问,先利用第一问的结论,得到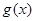 的解析式,再根据二次函数的单调性,确定对称轴与区间端点的大小关系解出
的解析式,再根据二次函数的单调性,确定对称轴与区间端点的大小关系解出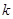 的取值.
的取值.试题解析:(1)∵
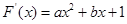 ,
,∴
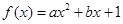 .
.∵
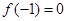 ,∴
,∴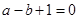 ,∴
,∴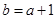 ,
,∴
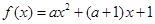 .∵
.∵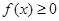 恒成立,
恒成立,∴
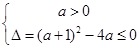 ∴
∴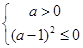
∴
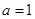 ,从而
,从而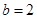 ,∴
,∴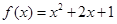 .(6分)
.(6分)(2)
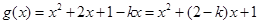 .
.∵
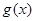 在
在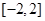 上是单调函数,
上是单调函数,∴
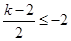 或
或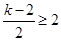 ,解得
,解得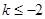 ,或
,或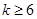 .
.∴
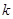 的取值范围为
的取值范围为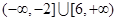 .(12分)
.(12分)
