题目
已知函数
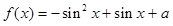 ,若
,若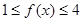 对一切
对一切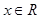 恒成立.求实数
恒成立.求实数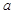 的取值范围.(16分)
的取值范围.(16分)
答案
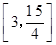 .
.
解析
试题分析:∵
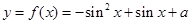 ,
,令
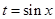 ,则
,则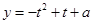 (
(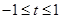 ),
),由于
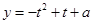 的对称轴是
的对称轴是 ,
,∴在
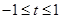 上,根据二次函数的单调性,有:
上,根据二次函数的单调性,有:当
 时,
时,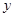 取得最大值,
取得最大值,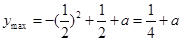 ,
,当
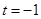 时,
时,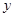 取得最小值,
取得最小值,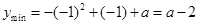 ,
,又∵
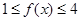 对一切
对一切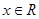 恒成立,
恒成立,即:
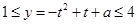 对一切
对一切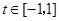 恒成立,
恒成立,所以有:
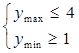 ,即
,即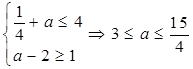 ,
,∴实数
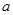 的取值范围是
的取值范围是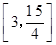 .
.点评:对于二次函数f(x)=ax2+bx+c=0(a≠0)在实数集R上恒成立问题可利用判别式直接求解,即 :f(x)>0恒成立
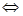

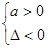 ;f(x)<0恒成立
;f(x)<0恒成立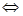

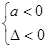 ,若是二次函数在指定区间上的恒成立问题,还可以利用韦达定理以及根与系数的分布知识求解.
,若是二次函数在指定区间上的恒成立问题,还可以利用韦达定理以及根与系数的分布知识求解.
