题目
(Ⅰ)已知函数
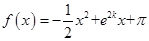 在
在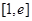 上具有单调性,求实数
上具有单调性,求实数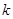 的取值范围;
的取值范围;(Ⅱ)已知向量
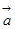 、
、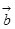 、
、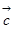 两两所成的角相等,且
两两所成的角相等,且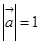 ,
,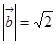 ,
,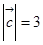 ,求
,求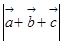 .
.
答案
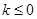 或
或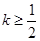 (Ⅱ)
(Ⅱ)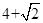 或
或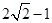
解析
试题分析:(Ⅰ)因为函数
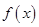 是二次函数,其图象对称轴为
是二次函数,其图象对称轴为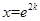
又
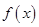 在
在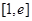 上具有单调性,
上具有单调性,所以
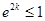 或
或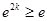 ,
,解得
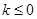 或
或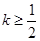 ,
,故实数
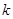 的取值范围是
的取值范围是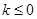 或
或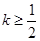 .
. (Ⅱ)当 向量
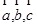 两两所成的角为
两两所成的角为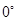 时,
时,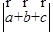 =
=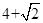
当 向量
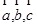 两两所成的角为
两两所成的角为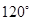 时,
时,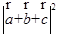 =
=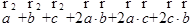
=
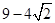
所以
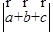 =
=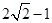
故
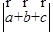 =
=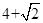 或
或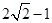
点评:第一问中考查二次函数的性质和应用,是基础题.解题的关键是灵活应用二次函数的性质,第二问中主要把握好向量模和数量积间的转化.
