题目
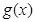 对任意实数
对任意实数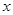 都满足
都满足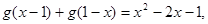 且
且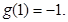
(Ⅰ)求
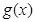 的表达式;
的表达式;(Ⅱ)设
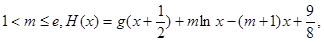 求证:
求证: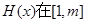 上为减函数;
上为减函数;(Ⅲ)在(Ⅱ)的条件下,证明:对任意
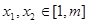 ,恒有
,恒有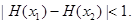
答案
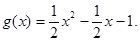 (Ⅱ)见解析(Ⅲ)见解析
(Ⅱ)见解析(Ⅲ)见解析
解析
试题分析:(1)设
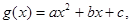
于是
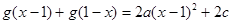

所以
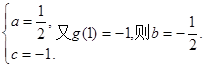
所以
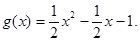 ………………5分
………………5分(2)
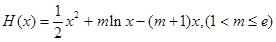 …………6分
…………6分因为对
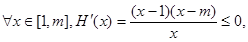
故
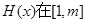 上为减函数 ………………8分
上为减函数 ………………8分(3)由(2)得:
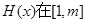 上为减函数则:
上为减函数则: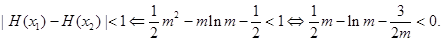 …………10分
…………10分记
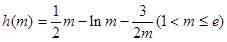 ,
,则
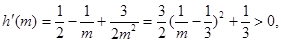 ………………11分
………………11分所以
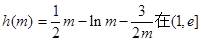 是单调增函数,
是单调增函数,所以
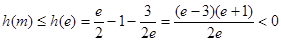 ,故命题成立 …………12分
,故命题成立 …………12分点评:(Ⅲ)中证明不等式恒成立转化为求函数最值问题,这是一种常用的转化思路
