题目
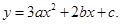
(1)若
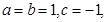 求该抛物线与
求该抛物线与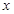 轴公共点的坐标;
轴公共点的坐标;(2)若
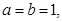 且当
且当 时,抛物线与
时,抛物线与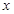 轴有且只有一个公共点,求c的取值范围;
轴有且只有一个公共点,求c的取值范围;(3)若
 且
且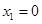 时,
时,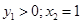 时,
时,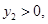 试判断当
试判断当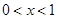 时,抛物线与
时,抛物线与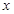 轴是否有公共点?若有,请证明你的结论;若没有,说明理由.
轴是否有公共点?若有,请证明你的结论;若没有,说明理由.
答案
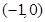 和
和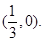 (2)当
(2)当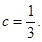 或
或 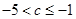 时,抛物线在
时,抛物线在 时与
时与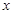 轴有且只有一个公共点. (3)当
轴有且只有一个公共点. (3)当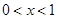 时,抛物线与
时,抛物线与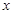 轴有两个公共点.
轴有两个公共点.
解析
(1)将a、b、c的值代入抛物线后求得解析式,令y=0求出x的值就是交点坐标的横坐标;
(2)根据其在此范围内有一个交点,此时将两个值代入,分别大于零和小于零,进而求出相应的取值范围.
(3)因为由题意可得,当
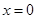 时,
时,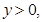 即
即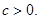 当
当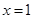 时,
时,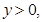
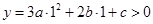
结合
 可得
可得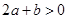 ,
,因为

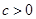 ,所以
,所以 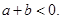 分析得到a,b的符号,然后结合判别式判定交点问题。
分析得到a,b的符号,然后结合判别式判定交点问题。解:(1)当
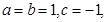 抛物线
抛物线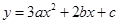 为
为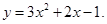
令
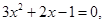 解得,
解得,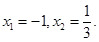
所以,抛物线
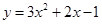 与
与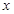 轴的公共点的坐标为
轴的公共点的坐标为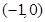 和
和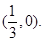 ……2分
……2分(2)当
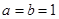 时,抛物线
时,抛物线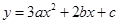 为
为 .
.令
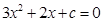 ,解之,得
,解之,得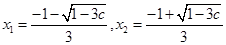 .
.①若抛物线与
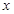 轴只有一个公共点,由题意,
轴只有一个公共点,由题意,可得
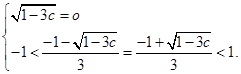 解之,得
解之,得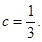
②若抛物线与
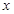 轴有两个公共点,由题意,可得
轴有两个公共点,由题意,可得 或
或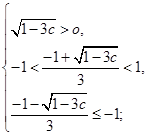
所以,
 或
或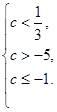 故
故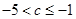 .
.综上所述,当
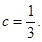 或
或 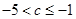 时,
时,抛物线在
 时与
时与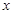 轴有且只有一个公共点. ……..8分
轴有且只有一个公共点. ……..8分(3)由题意可得,当
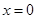 时,
时,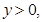 即
即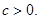 当
当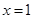 时,
时,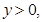
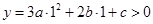
结合
 可得
可得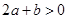 ,
,因为

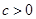 ,所以
,所以 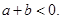
又
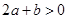 , 所以
, 所以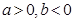 ……10分
……10分令
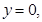 即
即  所以,此方程的判别式为
所以,此方程的判别式为 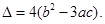
因为
 所以
所以 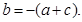 所以
所以 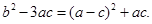
因为
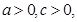 所以
所以 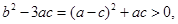 故
故 
所以 抛物线与
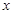 轴有且只有两个不同的交点. ……….13分
轴有且只有两个不同的交点. ……….13分因为,
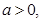 所以抛物线
所以抛物线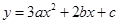 的顶点的纵坐标小于零。
的顶点的纵坐标小于零。因为
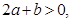
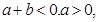 所以
所以 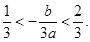
因为 抛物线的对称轴为
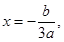 所以
所以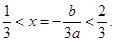
又当
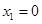 时,
时,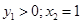 时,
时,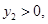 所以当
所以当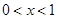 时,
时,抛物线与
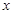 轴有两个公共点. ……16分
轴有两个公共点. ……16分
