题目
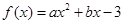 在
在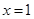 处取得极值,且在
处取得极值,且在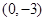 点处的切线与直线
点处的切线与直线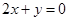 平行.
平行. (1)求
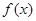 的解析式; (2)求函数
的解析式; (2)求函数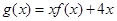 的单调递增区间及极值;
的单调递增区间及极值;(3)求函数
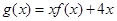 在
在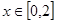 的最值.
的最值.
答案
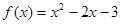 .
. (2)
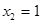 有极小值为0. 在
有极小值为0. 在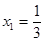 有极大值
有极大值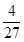 .
. (3)由
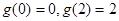 及(2),得,函数
及(2),得,函数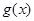 的最大值为2,最小值为0.
的最大值为2,最小值为0.
解析
(1)由f(x)=ax2+bx-3,知f′(x)=2ax+b.由二次函数f(x)=ax2+bx-3在x=1处取得极值,且在(0,-3)点处的切线与直线2x+y=0平行,知 f′(1)=2a+b=0,f′(0)=b=-2
,由此能求出f(x).(2)由f(x)=x2-2x-3,知g(x)=xf(x)+4x=x3-2x2+x,所以g′(x)=3x2-4x+1=(3x-1)(x-1).令g′(x)=0,得x1=
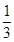 ,x2=1.列表讨论能求出函数g(x)=xf(x)+4x的单调递增区间及极值.
,x2=1.列表讨论能求出函数g(x)=xf(x)+4x的单调递增区间及极值.(3)由g(0)=0,g(2)=2,结合(2)的结论,能求出函数g(x)的最大值和最小值.
