题目
 在区间[0,1]上的最大值为2,求
在区间[0,1]上的最大值为2,求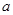 的值.
的值.
答案
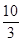 或-6.
或-6.
解析
需要对于函数对称轴与定义域的关系分类讨论得到结论。分为三种情况来得到。
解: f(x)=-
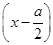 2+
2+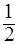 -
-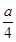 +
+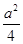 .
.①当
 ∈[0,1],即0≤a≤2时,f(x)max=
∈[0,1],即0≤a≤2时,f(x)max=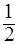 -
-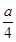 +
+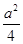 =2,
=2,则a=3或a=-2,不合题意.
②当
 >1时,即a>2时,f(x)max=f(1)=2⇒a=
>1时,即a>2时,f(x)max=f(1)=2⇒a=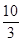 .
.③当
 <0时,即a<0时,f(x)max=f(0)=2⇒a=-6.
<0时,即a<0时,f(x)max=f(0)=2⇒a=-6.综上,f(x)在区间[0,1]上的最大值为2时a=
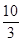 或-6.
或-6.
