题目
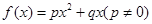 ,其导函数为
,其导函数为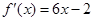 ,数列
,数列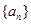 的前
的前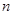 项和为
项和为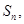 点
点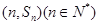 均在函数
均在函数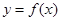 的图像上;.
的图像上;.(Ⅰ)求数列
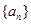 的通项公式;
的通项公式;(Ⅱ)若
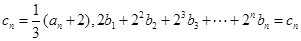 ,求数列
,求数列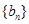 的通项公式;
的通项公式;(Ⅲ)已知不等式
 成立,
成立,求证:
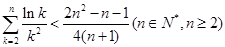
答案
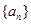 的通项公式:
的通项公式: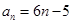
(Ⅱ)数列
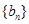 的通项公式:
的通项公式: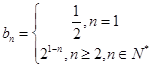
(Ⅲ)略
解析
(1)因为二次函数
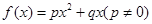 ,则
,则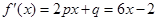 ,得到参数a,b的值。
,得到参数a,b的值。(2)由(Ⅰ)得,
 ,
, ,然后利用前n项和与通项公式的关系式得到结论。
,然后利用前n项和与通项公式的关系式得到结论。(3)已知不等式
 成立,故
成立,故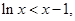 则
则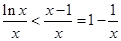 ……1分
……1分所以
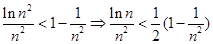 ,运用放缩法证明不等式
,运用放缩法证明不等式
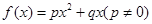 ,其导函数为
,其导函数为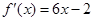 ,数列
,数列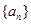 的前
的前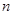 项和为
项和为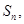 点
点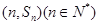 均在函数
均在函数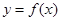 的图像上;.
的图像上;.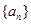 的通项公式;
的通项公式;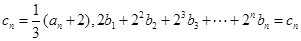 ,求数列
,求数列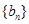 的通项公式;
的通项公式; 成立,
成立,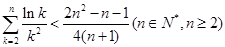
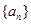 的通项公式:
的通项公式: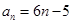
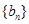 的通项公式:
的通项公式: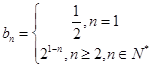
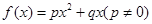 ,则
,则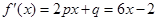 ,得到参数a,b的值。
,得到参数a,b的值。 ,
, ,然后利用前n项和与通项公式的关系式得到结论。
,然后利用前n项和与通项公式的关系式得到结论。 成立,故
成立,故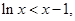 则
则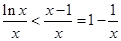 ……1分
……1分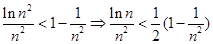 ,运用放缩法证明不等式
,运用放缩法证明不等式