题目
画出函数
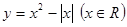 的图像,并指出它的单调区间.
的图像,并指出它的单调区间.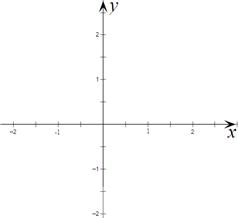
答案
单调减区间:(-∞,-1),(0,1).
解析
解:
 ∵f(-x)=(-x)2-|-x|=x2-|x|=f(x),
∵f(-x)=(-x)2-|-x|=x2-|x|=f(x),∴f(x)=x2-|x|为偶函数,∴函数f(x)=x2-2|x|的图象关于y轴对称;∴函数f(x)=x2-|x|的单调增区间:(-1,0),(1,+∞);
单调减区间:(-∞,-1),(0,1).
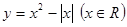 的图像,并指出它的单调区间.
的图像,并指出它的单调区间.
 ∵f(-x)=(-x)2-|-x|=x2-|x|=f(x),
∵f(-x)=(-x)2-|-x|=x2-|x|=f(x),