题目
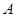 、
、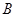 为函数
为函数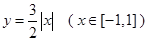 图象上不同的两个点,
图象上不同的两个点,且 AB∥
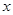 轴,又有定点
轴,又有定点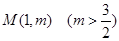 ,已知
,已知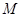 是线段
是线段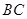 的中点.
的中点.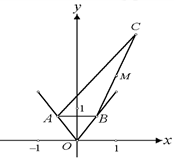
⑴ 设点
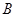 的横坐标为
的横坐标为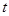 ,写出
,写出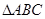 的面积
的面积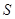 关于
关于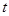 的函数
的函数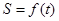 的表达式;
的表达式;⑵ 求函数
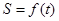 的最大值,并求此时点
的最大值,并求此时点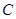 的坐标。
的坐标。
答案
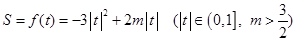 ;
;⑵当
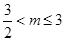 时,
时,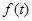 有最大值
有最大值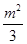 ,此时,点
,此时,点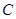 的坐标为
的坐标为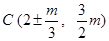 ;
;当
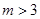 时,
时,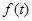 有最大值
有最大值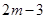 ,此时,点
,此时,点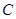 的坐标为
的坐标为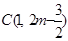 或
或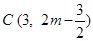 。
。
解析
(1)设
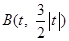 ,由
,由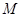 是线段
是线段 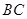 的中点,且
的中点,且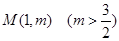 ,可推得点
,可推得点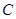 的坐标为
的坐标为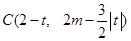 .
.进而表示其面积的表达式。
(2)由上知:
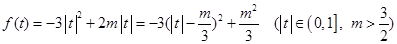
对参数m进行讨论得到最值。
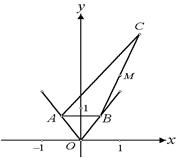
解:⑴ 如图,设
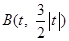 ,由
,由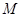 是线段
是线段 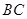 的中点,且
的中点,且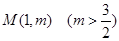 ,可推得点
,可推得点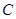 的坐标为
的坐标为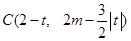 .
.
∴
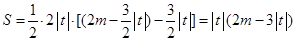
即:
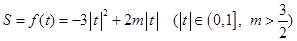 …(6分)
…(6分)⑵ 由上知:
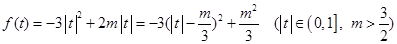
① 当
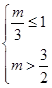 即
即 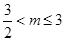 时,令
时,令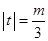 ,
,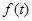 有最大值
有最大值 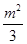 ,
,此时,点
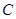 的坐标为
的坐标为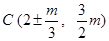 ;
;② 当
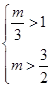 即
即 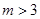 时,令
时,令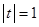 ,
,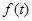 有最大值
有最大值 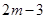 ,此时,点
,此时,点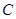 的坐标为
的坐标为 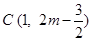 或
或 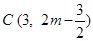 …….(12分)
…….(12分)纵上,当
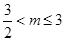 时,
时,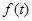 有最大值
有最大值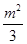 ,此时,点
,此时,点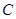 的坐标为
的坐标为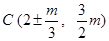 ;
;当
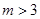 时,
时,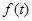 有最大值
有最大值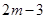 ,此时,点
,此时,点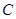 的坐标为
的坐标为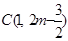 或
或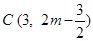 …(13分)
…(13分)
