题目
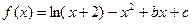 .
.(Ⅰ)若函数
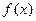 在
在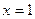 处的切线与直线
处的切线与直线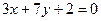 垂直,且
垂直,且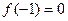 ,求函数
,求函数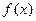 的解析式;
的解析式;(Ⅱ)若
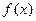 在区间
在区间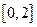 上单调递减,求
上单调递减,求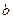 的取值范围.
的取值范围.
答案
(1)
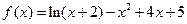
(2)
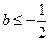
解析
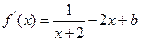 ,由
,由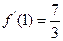 ,
,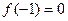 得
得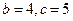 .所以
.所以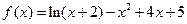 .
.(Ⅱ)
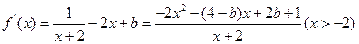 ,
,设
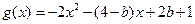 ,
,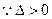 恒成立,故
恒成立,故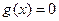 必有两根.
必有两根.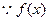 在区间
在区间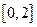 上单调递减,
上单调递减,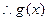 在
在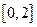 上值恒非正,
上值恒非正,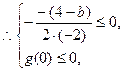 或
或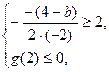 解得
解得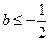 .
.故当
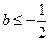 时,
时,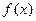 在
在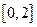 上单调递减.
上单调递减.
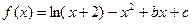 .
.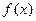 在
在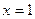 处的切线与直线
处的切线与直线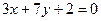 垂直,且
垂直,且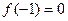 ,求函数
,求函数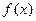 的解析式;
的解析式;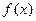 在区间
在区间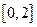 上单调递减,求
上单调递减,求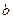 的取值范围.
的取值范围.
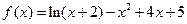
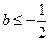
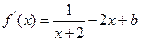 ,由
,由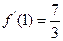 ,
,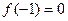 得
得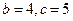 .所以
.所以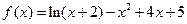 .
.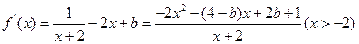 ,
,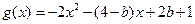 ,
,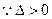 恒成立,故
恒成立,故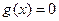 必有两根.
必有两根.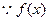 在区间
在区间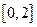 上单调递减,
上单调递减,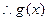 在
在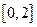 上值恒非正,
上值恒非正,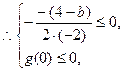 或
或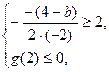 解得
解得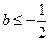 .
.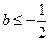 时,
时,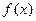 在
在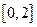 上单调递减.
上单调递减.