题目
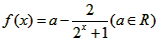
(1)是否存在实数a,使得函数f(x)是奇函数,若存在求出a值,不存在说明理由;
(2)判断函数f(x)的单调性,并证明
答案
解:(1)函数f(x)定义域为R,且f(x)是奇函数,所以f(0)=0=a-1
所以存在实数a=1使得函数f(x)是奇函数;
(2)函数f(x)在(-∞,+∞)上是增函数,证明如下:
设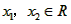 ,且
,且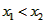 ,则
,则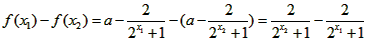
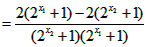
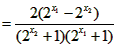
因为函数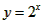 在R上是增函数,且y>0,又因为
在R上是增函数,且y>0,又因为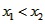 ,
,
所以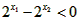 ,
,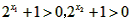 ,
,
所以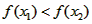 ,所以函数f(x)在(-∞,+∞)上是增函数
,所以函数f(x)在(-∞,+∞)上是增函数
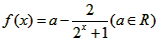
解:(1)函数f(x)定义域为R,且f(x)是奇函数,所以f(0)=0=a-1
所以存在实数a=1使得函数f(x)是奇函数;
(2)函数f(x)在(-∞,+∞)上是增函数,证明如下:
设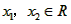 ,且
,且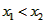 ,则
,则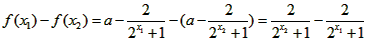
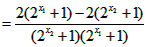
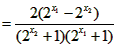
因为函数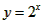 在R上是增函数,且y>0,又因为
在R上是增函数,且y>0,又因为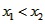 ,
,
所以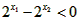 ,
,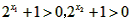 ,
,
所以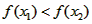 ,所以函数f(x)在(-∞,+∞)上是增函数
,所以函数f(x)在(-∞,+∞)上是增函数