题目
己知函数
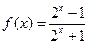 ,(Ⅰ)证明函数
,(Ⅰ)证明函数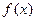 是R上的增函数;
是R上的增函数;(Ⅱ)求函数
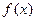 的值域.(Ⅲ)令
的值域.(Ⅲ)令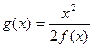 .判定函数
.判定函数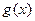 的奇偶性,并证明
的奇偶性,并证明
答案
解析
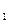 < x
< x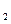 ,则△x= x
,则△x= x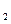 -x
-x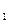 >0
>0△y=y
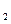 -y
-y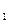 =f(x
=f(x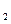 )-f(x
)-f(x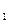 )=
)= 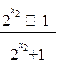 -
-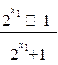
=
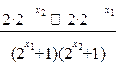 =
= 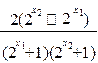 ………………………… (2分)
………………………… (2分)当x
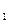 < x
< x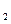 时,2
时,2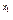 < 2
< 2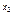 ∴2
∴2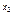 -2
-2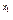 >0.又2
>0.又2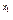 +1>0,2
+1>0,2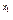 +1>0
+1>0∴△y>0,∴f ( x)是R上的增函数。…………………… (4分)
(Ⅱ)f(x)=
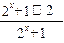 =1-
=1-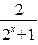 ……………………………………………(6分)
……………………………………………(6分)∵2
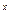 +1>1 ∴0<
+1>1 ∴0< 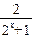 <2,即-2<-
<2,即-2<-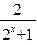 <0,就是-1<1-
<0,就是-1<1-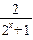 <1
<1∴f(x)的值域为(-1,1)……………………………………… (8分)
(Ⅲ)由题意知g(x)=
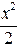 ·
·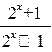 ………………(11分)
………………(11分)易知函数 g(x)的定义域为(-∞,0)∪(0,+∞)
g(-x)=
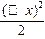 ·
·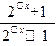 =
=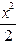 ·
·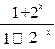 = -
= -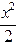 ·
·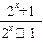 =-g(x)
=-g(x)∴函数g(x)为奇函数………………………………………………………………(14分)
