题目
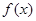 满足:对任意的
满足:对任意的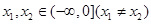 ,有
,有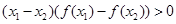 ,则当
,则当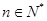 时,有
时,有A.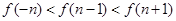
|
B.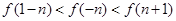
|
C.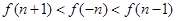
|
D.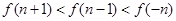
|
答案
解析
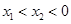 时,
时,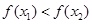 ,所以
,所以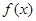 在
在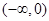 上单调递增。又因为
上单调递增。又因为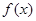 为偶函数,所以
为偶函数,所以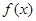 在
在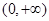 上单调递减,从而有:
上单调递减,从而有: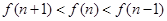
,又因为
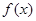 为偶函数,所以
为偶函数,所以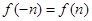 ,故选C。
,故选C。
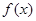 满足:对任意的
满足:对任意的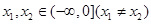 ,有
,有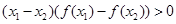 ,则当
,则当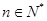 时,有
时,有A.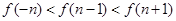
|
B.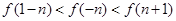
|
C.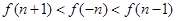
|
D.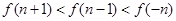
|
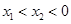 时,
时,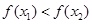 ,所以
,所以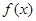 在
在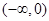 上单调递增。又因为
上单调递增。又因为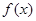 为偶函数,所以
为偶函数,所以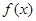 在
在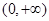 上单调递减,从而有:
上单调递减,从而有: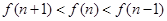
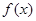 为偶函数,所以
为偶函数,所以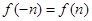 ,故选C。
,故选C。