题目
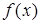 为奇函数, 且在(-∞, 0)内是减函数, f(-2)=" 0," 则
为奇函数, 且在(-∞, 0)内是减函数, f(-2)=" 0," 则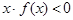 的解集为 ( )
的解集为 ( ) | A.(-1, 0)∪(2, +∞) | B.(-∞, -2)∪(0, 2 ) |
| C.(-∞, -2)∪(2, +∞) | D.(-2, 0)∪(0, 2 ) |
答案
解析
因为函数
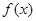 为奇函数, 且在
为奇函数, 且在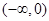 内是减函数,
内是减函数, 所以函数
所以函数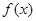 在
在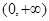 内也是减函数,且
内也是减函数,且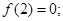 则不等式
则不等式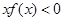 可化为
可化为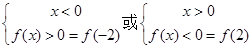 ,解得
,解得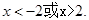 故选C
故选C
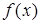 为奇函数, 且在(-∞, 0)内是减函数, f(-2)=" 0," 则
为奇函数, 且在(-∞, 0)内是减函数, f(-2)=" 0," 则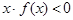 的解集为 ( )
的解集为 ( ) | A.(-1, 0)∪(2, +∞) | B.(-∞, -2)∪(0, 2 ) |
| C.(-∞, -2)∪(2, +∞) | D.(-2, 0)∪(0, 2 ) |
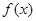 为奇函数, 且在
为奇函数, 且在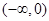 内是减函数,
内是减函数, 所以函数
所以函数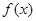 在
在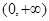 内也是减函数,且
内也是减函数,且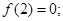 则不等式
则不等式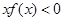 可化为
可化为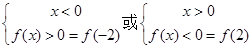 ,解得
,解得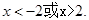 故选C
故选C