题目
(1)
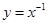 (2)
(2)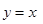 (3)
(3)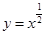 (4)
(4)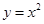 (5)
(5)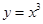
| A.1个 | B.2个 | C.3个 | D.4个 |
答案
解析
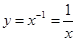 定义域为
定义域为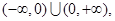 对定义域内任意
对定义域内任意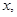
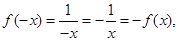 函数
函数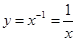 是奇函数;
是奇函数;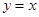 定义域为R,显然满足
定义域为R,显然满足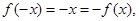 时奇函数;
时奇函数;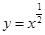 定义域为
定义域为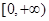 ,不关于原点对称,不具有奇偶性;
,不关于原点对称,不具有奇偶性;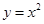 定义域为R,显然满足
定义域为R,显然满足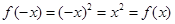 时偶函数;
时偶函数;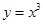 定义域为R,满足
定义域为R,满足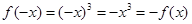 时奇函数.
时奇函数.故选C
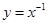 (2)
(2)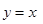 (3)
(3)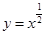 (4)
(4)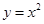 (5)
(5)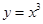
| A.1个 | B.2个 | C.3个 | D.4个 |
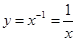 定义域为
定义域为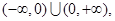 对定义域内任意
对定义域内任意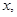
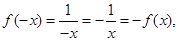 函数
函数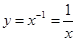 是奇函数;
是奇函数;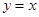 定义域为R,显然满足
定义域为R,显然满足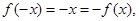 时奇函数;
时奇函数;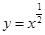 定义域为
定义域为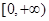 ,不关于原点对称,不具有奇偶性;
,不关于原点对称,不具有奇偶性;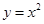 定义域为R,显然满足
定义域为R,显然满足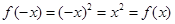 时偶函数;
时偶函数;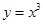 定义域为R,满足
定义域为R,满足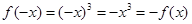 时奇函数.
时奇函数.