题目
 2分)判断函数y=
2分)判断函数y=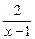 在区间[2,6]上的单调性,并求最大值和最小值.
在区间[2,6]上的单调性,并求最大值和最小值.
答案
f(x1)-f(x2)=
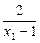 -
-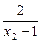 =
=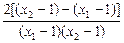 =
=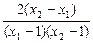 .
.由2<x1<x2<6,得x2-x1>0,(x1-1)(x2-1)>0,
于是f(x1)-f(x2)
 >0,即f(x1)>f(x2). xx_
>0,即f(x1)>f(x2). xx_所以函数y=
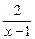 是区间[2,6]上的减函数.
是区间[2,6]上的减函数.因此,函数y=
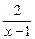 在区间的两个端点上分别取得最大值与最小值,即当x=2时,ymax=2;当x=6时,ymin=
在区间的两个端点上分别取得最大值与最小值,即当x=2时,ymax=2;当x=6时,ymin=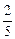 .
.
 2分)判断函数y=
2分)判断函数y=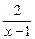 在区间[2,6]上的单调性,并求最大值和最小值.
在区间[2,6]上的单调性,并求最大值和最小值.
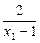 -
-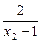 =
=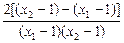 =
=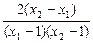 .
. >0,即f(x1)>f(x2). xx_
>0,即f(x1)>f(x2). xx_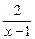 是区间[2,6]上的减函数.
是区间[2,6]上的减函数.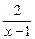 在区间的两个端点上分别取得最大值与最小值,即当x=2时,ymax=2;当x=6时,ymin=
在区间的两个端点上分别取得最大值与最小值,即当x=2时,ymax=2;当x=6时,ymin=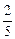 .
.