题目
 是定义在R上的奇函数,对任意实数
是定义在R上的奇函数,对任意实数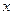 有
有 成立.
成立.(1)证明
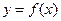 是周期函数,并指出其周期;
是周期函数,并指出其周期;(2)若
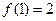 ,求
,求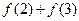 的值;
的值;(3)若
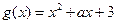 ,且
,且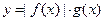 是偶函数,求实数
是偶函数,求实数 的值.
的值.
答案
 ,且
,且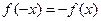 知
知 ,
,所
 以
以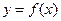 是周期函数,且
是周期函数,且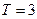 是其一个周期.
是其一个周期.(2)因为
 为定义在R上的奇函数,所以
为定义在R上的奇函数,所以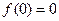 ,且
,且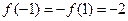 ,又
,又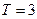 是
是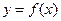 的一个周期,所以
的一个周期,所以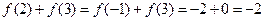 ;
;(3)因为
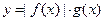 是偶函数,且可证明
是偶函数,且可证明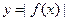 是偶函数,所以
是偶函数,所以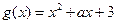 为偶函数,即
为偶函数,即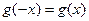 恒成立.
恒成立.于是
 恒成立,于是
恒成立,于是 恒成立
恒成立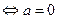 ,
,所以
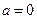 为所求.
为所求.
 是定义在R上的奇函数,对任意实数
是定义在R上的奇函数,对任意实数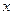 有
有 成立.
成立.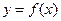 是周期函数,并指出其周期;
是周期函数,并指出其周期;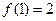 ,求
,求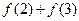 的值;
的值;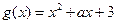 ,且
,且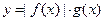 是偶函数,求实数
是偶函数,求实数 的值.
的值.
 ,且
,且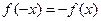 知
知 ,
, 以
以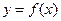 是周期函数,且
是周期函数,且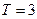 是其一个周期.
是其一个周期. 为定义在R上的奇函数,所以
为定义在R上的奇函数,所以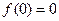 ,且
,且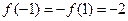 ,又
,又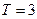 是
是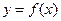 的一个周期,所以
的一个周期,所以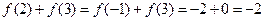 ;
;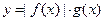 是偶函数,且可证明
是偶函数,且可证明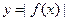 是偶函数,所以
是偶函数,所以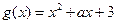 为偶函数,即
为偶函数,即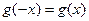 恒成立.
恒成立. 恒成立,于是
恒成立,于是 恒成立
恒成立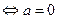 ,
,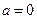 为所求.
为所求.