题目
 是奇函数,且f(2)=
是奇函数,且f(2)=
(1)求实数m,n的值;
(2)判断f(x)在(﹣∞,﹣1)的单调性,并加以证明.
答案
所以有f(﹣x)=﹣f(x)
∴
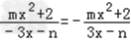
∴3x+n=3x﹣n
∵n=0∴
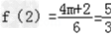
∴m=2∴m=2n=0
(2)f(x)=
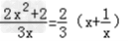 在(﹣∞,﹣1)上为增函数.
在(﹣∞,﹣1)上为增函数.证明:设x1,x2∈(﹣∞,﹣1)且x1<x2
则f(x1)﹣f(x2)=
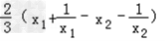
=
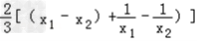
=
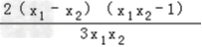
∵x1<x2<﹣1
∴x1x2>1,x1﹣x2<0
∴
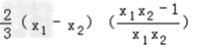 <0
<0∴f(x1)﹣f(x2)<0
所以f(x)在(﹣∞,﹣1)的单调增函数.
 是奇函数,且f(2)=
是奇函数,且f(2)=
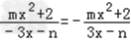
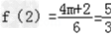
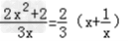 在(﹣∞,﹣1)上为增函数.
在(﹣∞,﹣1)上为增函数.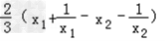
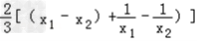
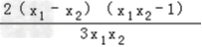
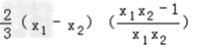 <0
<0