题目

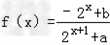已知定义域为R的函数是奇函数．
（Ⅰ）求a，b的值；
（Ⅱ）若对任意的t∈R，不等式f（t²﹣2t）+f（2t²﹣k）＜0恒成立，求k的取值范围．

答案

解：（Ⅰ）因为f（x）是奇函数，所以f（0）=0，
即
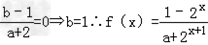
又由f（1）=﹣f（﹣1）知
．
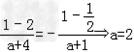所以a=2，b=1．
（Ⅱ）由（Ⅰ）知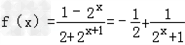，易知f（x）在（﹣∞，+∞）上为减函数．
又因为f（x）是奇函数，
所以f（t²﹣2t）+f（2t²﹣k）＜0等价于f（t²﹣2t）＜﹣f（2t²﹣k）=f（k﹣2t²），
因为f（x）为减函数，由上式可得：t²﹣2t＞k﹣2t²．
即对一切t∈R有：3t²﹣2t﹣k＞0，从而判别式．
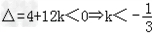k的取值范围是k＜﹣．

解析