题目

已知函数f（x）是定义在R上的偶函数，且x≧0时，．
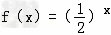（I）求f（-1）的值；
（II）求函数f（x）的值域A；
（III）设函数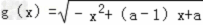的定义域为集合B，若A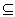B，求实数a的取值范围．

答案

解：（I）∵函数f（x）是定义在R上的偶函数
∴f（-1）=f（1）
又x≥0时，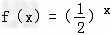
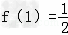∴，即f（-1）=．
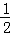（II）由函数f（x）是定义在R上的偶函数，可得函数f（x）的值域A即为
x≧0时，f（x）的取值范围，
当x≧0时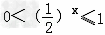，故函数f（x）的值域A=（0，1]．
（III）∵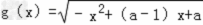
定义域B={x|﹣x²+（a﹣1）x+a≧0}={x|x²-（a﹣1）x﹣a≦0}
由x²-（a-1）x-a≦0
得（x-a）（x+1）≦0
∵A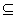B
∴B=[-1，a]，且a≧1
∴实数a的取值范围是{a|a≧1}

解析