题目

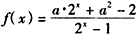已知函数（x∈R，x≠0），其中a为常数，且a＜0，
(Ⅰ)若f(x)是奇函数，求a的取值集合A；
(Ⅱ)当a=-1时，设f(x)的反函数为f^-1(x)且函数y=g(x)的图象与y=f^-1(x+1)的图象关于y=x对称，求g(1)的取值集合B：
(Ⅲ)对于问题(Ⅰ)(Ⅱ)中的A，B，当a∈{a|a＜0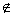，aA，a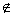B}时，不等式x²-10x+9＜a(x-4)恒成立，求x的取值范围。

答案

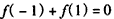解：(Ⅰ)由必要条件，得，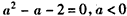
所以，a=-1，
下面证明充分性，当a=-1时，，
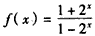任取x≠0，x∈R，
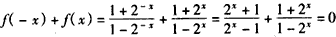恒成立，
则A={-1}。
(Ⅱ)当a=-1时，由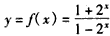得，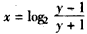
互换x，y得，
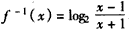则，
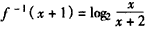从而，
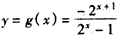所以，，
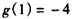所以，B={-4}。
(Ⅲ)原问题转化为，
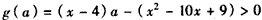a∈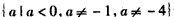恒成立，
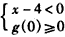则或，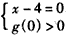
则x的取值范围为[1，4]。

解析